
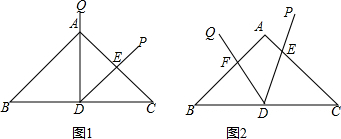
分析 (1)由等腰三角形的性质得出∠B=∠C,∠ADB=∠ADC=90°,因此△ABD∽△ACD,证出∠PDQ=∠C,由∠DAE=∠CAD,得出△ADE∽△ACD;在证出△CDE∽△CAD,即可得出结果;
(2)证出△BDF∽△CDE,得出对应边成比例$\frac{BF}{CD}=\frac{BD}{CE}$,即可得出y与x的函数关系式;
(3)由(2)可知:△BDF∽△CDE,得出$\frac{DF}{DE}=\frac{BD}{CE}$,证出$\frac{DF}{DE}=\frac{CD}{CE}$,由∠EDF=∠C,即可得出△DEF∽△CED.
解答 解:(1)与△CDE相似的三角形为△ABD,△ACD,△ADE;理由如下:
∵AB=AC,D为底边BC的中点,
∴∠B=∠C,AD⊥BC,
∴∠ADB=∠ADC=90°,
∴△ABD∽△ACD,
∵∠PDQ=∠B,
∴∠PDQ=∠C,
又∵∠DAE=∠CAD,
∴△ADE∽△ACD;
∵∠CDE+∠PDQ=90°,
∴∠C+∠PDQ=90°,
∴∠CED=90°=∠ADC,
又∵∠C=∠C,
∴△CDE∽△CAD,
∴△△ABD∽△ACD∽△ADE∽△CDE;
(2)∵∠FDC=∠B+∠BDF,
∠FDC=∠FDE+∠EDC,
∴∠EDC=∠BDF,
∴△BDF∽△CDE,
∴$\frac{BF}{CD}=\frac{BD}{CE}$,
∵D为BC的中点,
∴BD=CD=6,
∴$\frac{10-x}{6}=\frac{6}{10-y}$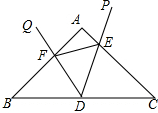
∴y=$\frac{10x-64}{x-10}$;
(3)△DEF与△CDE相似.理由如下:如图所示:
由(2)可知:△BDF∽△CDE,
则$\frac{DF}{DE}=\frac{BD}{CE}$,
∵BD=CD,
∴$\frac{DF}{DE}=\frac{CD}{CE}$,
又∵∠EDF=∠C,
∴△DEF∽△CED.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、等腰三角形的性质、三角形的外角性质等知识;本题综合性强,有一定难度,熟练掌握等腰三角形的性质,证明三角形相似得出比例式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
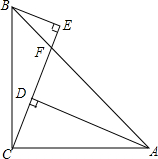 如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)
如图,AD=CE=24,BC=25,∠BCE=∠CAD,BE∥AD,BF:AF=7:24,给出下列结论:①∠E=90°;②∠BCA=90°;③∠BAC=45°;④AB=25$\sqrt{3}$.其中正确的结论有①②③.(把所有正确结论序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2,-1,0 | B. | -1,0,1 | C. | -1,0 | D. | -2,-1,0,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.11×104 | B. | 11.1×104 | C. | 1.11×105 | D. | 1.11×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
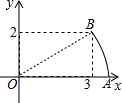 如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )
如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )| A. | 2和3之间 | B. | 3和3.5之间 | C. | 3.5和4之间 | D. | 4和5之间 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com