
 如图,已知两个不平行的向量$\overrightarrow a,\overrightarrow b$.先化简,再求作:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$.
如图,已知两个不平行的向量$\overrightarrow a,\overrightarrow b$.先化简,再求作:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$.分析 首先利用平面向量的加减运算法则化简原式,再利用三角形法则画出图形.
解答 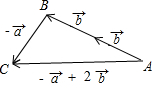 解:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$=$\frac{1}{2}$$\overrightarrow{a}$+3$\overrightarrow{b}$-$\frac{3}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$.
解:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$=$\frac{1}{2}$$\overrightarrow{a}$+3$\overrightarrow{b}$-$\frac{3}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$.
如图:$\overrightarrow{AB}$=2$\overrightarrow{b}$,$\overrightarrow{BC}$=-$\overrightarrow{a}$,
则$\overrightarrow{AC}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$,
即$\overrightarrow{AC}$即为所求.
点评 此题考查了平面向量的运算法则以及作法.注意作图时准确利用三角形法则是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
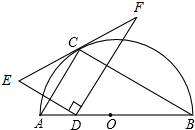 如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点,
如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-a}{2b}=\frac{a}{-2b}$ | B. | $\frac{1}{n}=\frac{m+1}{m+n}$ | C. | $\frac{{y}^{2}+y}{xy}=\frac{y+1}{xy}$ | D. | $\frac{a}{b}=\frac{a{c}^{2}}{b{c}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com