
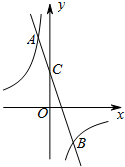
 如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-$\frac{6}{x}$的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.分析 (1)把点A(-1,m),B(n,-3)代入$y=-\frac{6}{x}$求得A(-1,6),B(2,-3),由于一次函数y=kx+b的图象过A(-1,6),B(2,-3)两点,解方程组,即可得到结果;
(2)由于一次函数y=-3x+3与y轴交点C(0,3)且B(2,-3)求得△BOC面积=3,由于P是x轴上一点,且△BOP的面积是△BOC面积的2倍,设P(a,0),得到方程$\frac{1}{2}$×|a|×2=6,解得即可得到结果.
解答 解:(1)∵点A(-1,m),B(n,-3)在反比例函数$y=-\frac{6}{x}$的图象上,
∴m=$\frac{-6}{-1}$=6,-3=$\frac{-6}{n}$,∴n=2.
∴A(-1,6),B(2,-3),
∵一次函数y=kx+b的图象过A(-1,6),B(2,-3)两点,
∴$\left\{{\begin{array}{l}{6=-k+b}\\{-3=2k+b}\end{array}}\right.$,解方程组得$\left\{{\begin{array}{l}{k=-3}\\{b=3}\end{array}}\right.$
∴一次函数的解析式为y=-3x+3;
(2)∵一次函数y=-3x+3与y轴交点C(0,3),且B(2,-3)
∴△BOC面积=3,
∵P是x轴上一点,且△BOP的面积是△BOC面积的2倍,
∴设P(a,0),
∴$\frac{1}{2}$×|a|×3=6,解得,a=±4.
∴点P的坐标为(4,0)或(-4,0).
点评 本题考查了待定系数法求函数的解析式,根据函数的解析式求点的坐标,根据三角形的面积求点的坐标,注意数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
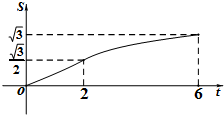 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )| A. | 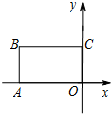 | B. | 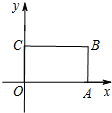 | C. | 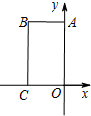 | D. | 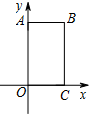 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
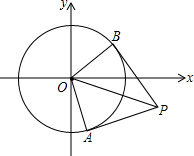 如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$.
如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
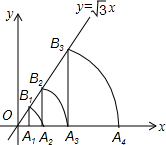 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
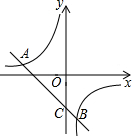 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A (-3,1),B (1,n)两点.
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A (-3,1),B (1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
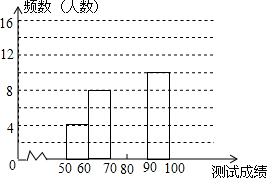 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
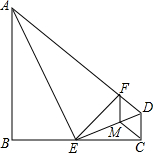 已知四边形ABCD中,∠ABC=90°,AB∥CD,BC=12,AB>6,点E为BC的中点,连接AE,ED,△ABE与△AFE关于直线AE对称,且点F在AD上
已知四边形ABCD中,∠ABC=90°,AB∥CD,BC=12,AB>6,点E为BC的中点,连接AE,ED,△ABE与△AFE关于直线AE对称,且点F在AD上查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com