
 如图,抛物线y=ax2+bx-16a+4b交x轴负半轴于点A,交x轴正半轴于点B,交y轴正半轴于点C,且OA:OB=2:3.
如图,抛物线y=ax2+bx-16a+4b交x轴负半轴于点A,交x轴正半轴于点B,交y轴正半轴于点C,且OA:OB=2:3.分析 (1)将原抛物线解析式分解因式,计算y=0时,方程的解为:x1=-4,x2=$\frac{4a-b}{a}$,得OA=4,由OA:OB=2:3,求出OB=6,写出点A、B的坐标;
(2)先根据:$\frac{4a-b}{a}$=6,求出a和b的关系:b=-2a,代入后得C(0,-24a),根据∠ABC=2∠ACO,作辅助线构建等腰三角形BGC,得∠ACO=∠CGB,利用等角的正切列式求出a的值,从而依次求出b和c的值,写出抛物线的解析式;
(3)作辅助线,构建梯形,根据解析式设P(x,-$\frac{1}{3}$x2+$\frac{2}{3}$x+8),则N(x,-$\frac{1}{2}$x+3),根据面积公式表示出△PMC和△PBD的面积,利用△PMC:△PBD的面积比为2:3或3:2列式可求得x的值.
解答 解:(1)y=ax2+bx-16a+4b,
=(ax2-16a)+(bx+4b),
=a(x+4)(x-4)+b(x+4),
=(x+4)(ax-4a+b),
当y=0时,(x+4)(ax-4a+b)=0,
x1=-4,x2=$\frac{4a-b}{a}$,
∵A在x轴负半轴上,
∴A(-4,0),
∴OA=4,
∵OA:OB=2:3,
∴OB=6,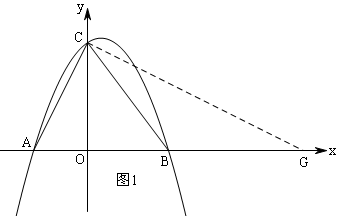
∴B(6,0);
(2)由(1)得:$\frac{4a-b}{a}$=6,
b=-2a,
当x=0时,y=-16a+4b=-24a,
∴C(0,-24a),
∴OC=-24a,
如图1,在x轴的正半轴上取一点G,使BC=BG,连接CG,
∴∠BCG=∠CGB,
∵∠ABC=∠BCG+∠CGB,
∴∠ABC=2∠CGB,
∵∠ABC=2∠ACO,
∴∠ACO=∠CGB,
tan∠ACO=tan∠CGB,
∴$\frac{AO}{OC}=\frac{OC}{OG}$,
在Rt△BCO中,BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{(-24a)^{2}+{6}^{2}}$=$\sqrt{576{a}^{2}+36}$,
∴$\frac{4}{-24a}$=$\frac{-24a}{6+\sqrt{576{a}^{2}+36}}$,
设576a2=m,则变形为:24+4$\sqrt{36+m}$=m,
解得:m1=0(舍),m2=64,
当m=64时,即576a2=64,a=$±\frac{1}{3}$,
由题意得:a<0,
∴a=-$\frac{1}{3}$,
∴b=-2a=$\frac{2}{3}$,
-24a=-24×(-$\frac{1}{3}$)=8,
∴抛物线的解析式为:y=-$\frac{1}{3}$x2+$\frac{2}{3}$x+8;
(3)如图2,
当x=0时,y=8,
∴C(0,8),
∴OC=8,
∵A(-4,0),B(6,0),
∴AB=10,
连接BC,
∴BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴BC=AB,
∵M是AC的中点,
∴BM⊥AC,∠ABM=∠CBM=$\frac{1}{2}$∠ABC=∠ACO,
∴tan∠ABM=tan∠ACO,
∴$\frac{OD}{OB}=\frac{OA}{OC}$,
∴$\frac{OD}{6}=\frac{4}{8}$,
∴OD=3,
∴D(0,3),
设BD的解析式为:y=kx+b,
把B(6,0)、D(0,3)代入得:$\left\{\begin{array}{l}{6k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$,
∴BD的解析式为:y=-$\frac{1}{2}$x+3,
过P作PH⊥OB于H,交BD于N,过M作MQ⊥OA于Q,
设P(x,-$\frac{1}{3}$x2+$\frac{2}{3}$x+8),则N(x,-$\frac{1}{2}$x+3),
∴PN=PH-NH=-$\frac{1}{3}$x2+$\frac{2}{3}$x+8-(-$\frac{1}{2}$x+3)=-$\frac{1}{3}{x}^{2}$+$\frac{7}{6}$x+5,
∴S△PBD=$\frac{1}{2}$PN•OB=$\frac{1}{2}$(-$\frac{1}{3}{x}^{2}$+$\frac{7}{6}$x+5)×6=-x2+$\frac{7}{2}$x+15,
∵M是AC的中点,
∴M(-2,4),
∴MQ=4,
∴S△PMC=S梯形MQOC+S梯形COHP-S梯形MQHP,
=$\frac{1}{2}$(4+8)×2+$\frac{1}{2}$(8-$\frac{1}{3}$x2+$\frac{2}{3}$x+8)•x-$\frac{1}{2}$(4-$\frac{1}{3}$x2+$\frac{2}{3}$x+8)(2+x),
=12+$\frac{x}{2}$(-$\frac{1}{3}$x2+$\frac{2}{3}$x+16)-(1+$\frac{1}{2}$x)(-$\frac{1}{3}$x2+$\frac{2}{3}$x+12),
=$\frac{1}{3}{x}^{2}$+$\frac{4}{3}$x,
若S△PMC:S△PBD=2:3,即2S△PBD=3△PMC,
则2(-x2+$\frac{7}{2}$x+15)=3($\frac{1}{3}{x}^{2}$+$\frac{4}{3}$x),
-2x2+7x+30=x2+4x,
3x2-3x-30=0,
x2-x-10=0,
x1=$\frac{1+\sqrt{41}}{2}$,x2=$\frac{1-\sqrt{41}}{2}$(舍),
∴P($\frac{1+\sqrt{41}}{2}$,$\frac{53+\sqrt{41}}{6}$),
若S△PMC:S△PBD=3:2,即3S△PBD=2S△PMC,
则3(-x2+$\frac{7}{2}$x+15)=2($\frac{1}{3}{x}^{2}$+$\frac{4}{3}$x),
-3x2+$\frac{21}{2}$x+45=$\frac{2}{3}{x}^{2}$+$\frac{8}{3}$x,
-18x2+63x+270=4x2+16x,
22x2-47x-270=0,
x1=$\frac{47+\sqrt{25969}}{44}$,x2=$\frac{47-\sqrt{25969}}{44}$(舍),
∴P($\frac{47+\sqrt{25969}}{44}$,$\frac{22827-3\sqrt{25969}}{2904}$),
综上所述,点P的坐标为:P($\frac{1+\sqrt{41}}{2}$,$\frac{53+\sqrt{41}}{6}$)或($\frac{47+\sqrt{25969}}{44}$,$\frac{22827-3\sqrt{25969}}{2904}$).
点评 本题是二次函数的综合题,主要考查了二次函数与两坐标轴的交点问题、因式分解,与一元二次方程的关系、勾股定理、三角形面积的不同表示方法等知识的综合应用能力;综合性较强,同时利用数形结合的思想解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
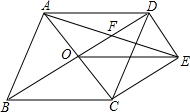 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.
如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE∥AC且DE=OC,连接CE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
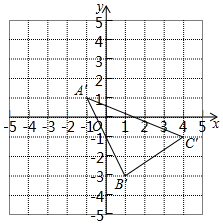 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a5)2=a7 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | 4a3•2a2=8a6 | D. | a8÷a2=a6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com