
 如图,在△ABC中,∠C=45°,BC=12,高AD=10,矩形EFPQ的一边QP边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在△ABC中,∠C=45°,BC=12,高AD=10,矩形EFPQ的一边QP边上,E、F两点分别在AB、AC上,AD交EF于点H.分析 (1)根据矩形的性质得出EF∥QP,再由AD⊥BC可得出AH⊥EF,进而可得出结论;
(2)先用x表示出AH的长,再由S矩形EFPQ=EF•EQ可得出二次函数的解析式,进而可得出结论;
(3)先求出PC及QC的长,再分0≤t≤5,5≤t<6及6≤t≤11三种情况进行讨论即可.
解答  (1)证明:∵四边形EFPQ是矩形,
(1)证明:∵四边形EFPQ是矩形,
∴EF∥QP.
∵AD⊥BC,
∴AH⊥EF,
∴$\frac{AH}{AD}$=$\frac{EF}{BC}$;
(2)解:∵由(1)得,$\frac{AH}{10}$=$\frac{x}{12}$,
∴AH=$\frac{5}{6}$x,
∴EQ=HD=AD-AH=10-$\frac{5}{6}$x,
∴S矩形EFPQ=EF•EQ=x(10-$\frac{5}{6}$x)=-$\frac{5}{6}$x2+10x=-$\frac{5}{6}$(x-6)2+30,
∵-$\frac{5}{6}$<0,
∴当x=6时,S矩形EFPQ有最大值,最大值为30.
(3)解:如图1,由(2)得,EF=6,EQ=5,
∵∠C=45°,
∴△FPC是等腰直角三角形,
∴PC=PF=EQ=5,QC=QP+PC=11,
分三种情况进行讨论:
①如图2所示,当0≤t≤5时,设EF、PF分别交AC于点M,则△MFN是等腰直角三角形,
∴FN=MF=t,
∴S=S矩形EFPQ-S△MFN=30-$\frac{1}{2}$t2=-$\frac{1}{2}$t2+30;
②如图3,当5≤t<6时,则ME=6-t,QC=11-t,
∴S=S梯形EMCQ=$\frac{1}{2}$[(6-t)+(11-t)]×5=-5t+$\frac{85}{2}$;
③如图4,当6≤t≤11时,设EQ交AC于点K,则△KQC是等腰直角三角形,则KQ=QC=11-t,
∴S=S△KQC=$\frac{1}{2}$(11-t)2,
综上所述,S与t的函数关系式为:
$S=\left\{\begin{array}{l}-\frac{1}{2}{t}^{2}+30(0≤t<5)\\-5t+\frac{85}{2}(5≤t<6)\\ \frac{1}{2}(t-1)^{2}(6≤t≤11)\end{array}\right.$.
点评 本题考查的是相似形综合题,涉及到等腰直角三角形的性质、矩形的性质及二次函数的最值问题,在解答(3)时要注意进行分类讨论.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
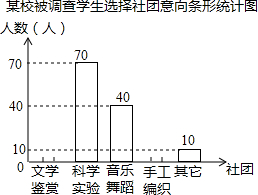 为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数中x和y的部分对应值如下表:
已知二次函数中x和y的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC.求证:∠1=∠E.
如图,已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC.求证:∠1=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 28 | B. | 36 | C. | 45 | D. | 55 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com