
���� �������֪$\frac{1}{1��3}$+$\frac{1}{3��5}$+��+$\frac{1}{99��101}$=$\frac{1}{2}$��1-$\frac{1}{3}$$+\frac{1}{3}$$-\frac{1}{5}$+��+$\frac{1}{99}-\frac{1}{101}$�����Ӷ�����ô𰸣�������������������ʽ���в�������Ӷ�����ô𰸣�
��� �⣺$\frac{1}{1��3}$+$\frac{1}{3��5}$+��+$\frac{1}{99��101}$=$\frac{1}{2}$��1-$\frac{1}{3}$$+\frac{1}{3}$$-\frac{1}{5}$+��+$\frac{1}{99}-\frac{1}{101}$��
=$\frac{1}{2}����1-\frac{1}{101}��$
=$\frac{1}{2}��\frac{100}{101}$
=$\frac{50}{101}$��
�ʴ�Ϊ��$\frac{50}{101}$��
$\frac{1}{x��x+2��}$+$\frac{1}{��x+2����x+4��}$+$\frac{1}{��x+4����x+6��}$+$\frac{1}{��x+6����x+8��}$=$\frac{1}{2}$��$\frac{1}{x}-\frac{1}{x+2}$��+$\frac{1}{2}��\frac{1}{x+2}-\frac{1}{x+4}��$+��+$\frac{1}{2}��\frac{1}{x+6}-\frac{1}{x+8}��$
=$\frac{1}{2}��$��$\frac{1}{x}-\frac{1}{x+8}$��
=$\frac{1}{2}��$$\frac{8}{x��x+8��}$
=$\frac{4}{x��x+8��}$��
���� ������Ҫ������Ƿ�ʽ�ļӼ������ݲ����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1=��3 | B�� | ��1=��2 | C�� | ��2=��3 | D�� | ��1=��2=��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3a-2a=1 | B�� | a+2a2=3a3 | C�� | -��a-b��=-a+b | D�� | 2��a+b��=2a+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 812��106 | B�� | 81.2��107 | C�� | 8.12��108 | D�� | 8.12��109 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | V=30P | B�� | P=V+900 | C�� | P=30V | D�� | PV=30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
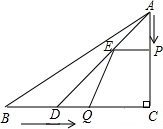 ��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=5cm����D��BC�ϣ���CD=3cm��������������P��Q�ֱ�ӵ�A�͵�Bͬʱ���������е�P��1����/����ٶ���AC���յ�C�˶�����Q��1.25����/����ٶ���BC���յ�C�˶�������P��PE��BC��AD�ڵ�E������EQ���趯���˶�ʱ��Ϊt�루t��0������һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶���
��ͼ����Rt��ABC�У���C=90�㣬AC=4cm��BC=5cm����D��BC�ϣ���CD=3cm��������������P��Q�ֱ�ӵ�A�͵�Bͬʱ���������е�P��1����/����ٶ���AC���յ�C�˶�����Q��1.25����/����ٶ���BC���յ�C�˶�������P��PE��BC��AD�ڵ�E������EQ���趯���˶�ʱ��Ϊt�루t��0������һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{16}$=��4 | B�� | $\sqrt{{{��-5��}^2}}$=-5 | C�� | ��$\sqrt{64}$=��8 | D�� | $\root{3}{-27}$=-9 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com