
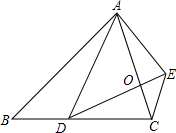
 已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.
已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.分析 (1)根据三角形的外角的性质和角的和差得到∠B=∠ADE,由于$\frac{BA}{BC}=\frac{DA}{DE}$=1,根据得到结论;
(2)根据相似三角形的性质得到∠BAC=∠DAE,于是得到∠BAD=∠CAE=∠CDE,证得△COD∽△EOA,根据相似三角形的性质得到$\frac{OC}{OE}=\frac{OD}{OA}$,由∠AOD=∠COE,推出△AOD∽△COE,根据相似三角形的性质即可得到结论.
解答 证明:(1)∵∠ADC=∠ABC+∠BAD=∠ADE+∠EDC,
∴∠B=∠ADE,
∵$\frac{BA}{BC}=\frac{DA}{DE}$=1,
∴△ABC∽△ADE;
(2)∵△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE=∠CDE,
∵∠COD=∠EOA,
∴△COD∽△EOA,
∴$\frac{OC}{OE}=\frac{OD}{OA}$,
∵∠AOD=∠COE,
∴△AOD∽△EOC,
∴DA:CE=OD:OC,
即DA•OC=OD•CE.
点评 本题考查了相似三角形的判定和性质,三角形的外角的性质,熟练掌握相似三角形的判定定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0.49968×105 | B. | 49.968×103 | C. | 4.9968×104 | D. | 4.9968×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
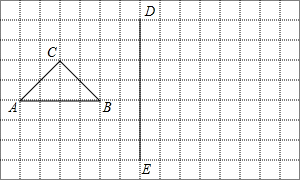 如图,在所给网格图(每小格均为边长为1的正方形),
如图,在所给网格图(每小格均为边长为1的正方形),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )| A. | 12cm | B. | 7cm | ||
| C. | 6cm | D. | 随直线MN的变化而变化 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
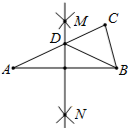 如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若∠A=25°,则∠CDB=( )
如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若∠A=25°,则∠CDB=( )| A. | 25° | B. | 50° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com