
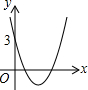
 已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b-1)x+3的图象可能是( )
已知二次函数y=x2+bx+3如图所示,那么函数y=x2+(b-1)x+3的图象可能是( )| A. | 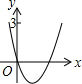 | B. | 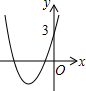 | C. |  | D. | 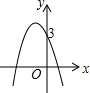 |
分析 根据函数y=x2+(b-1)x+3可知该函数的开口方向和一定过点(0,3),且通过变形可以与二次函数y=x2+bx+3建立关系,从而可以解答本题.
解答 解:∵函数y=x2+(b-1)x+3的a=1>0,过点(0,3),
∴该函数的图象开口向上,一定过点(0,3),
故选项A、D错误;
又∵二次函数y=x2+bx+3的图象已知,对称轴在y轴右侧,故可知b<0,所以b-1<0,
抛物线y=x2+(b-1)x+3的对称轴为x=$-\frac{b-1}{2}$>0,即对称轴也在y轴的右侧,
故选项B错误,选项C正确,
故选C.
点评 本题考查二次函数的图象,解题的关键是明确题意,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:选择题
| A. | 1cm,3cm,5cm | B. | 1cm,1cm,2cm | C. | 1cm,2cm,3cm | D. | 1cm,2cm,2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
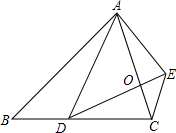 已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.
已知:如图,已知△ABC与△ADE均为等腰三角形,BA=BC,DA=DE.如果点D在BC边上,且∠EDC=∠BAD.点O为AC与DE的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
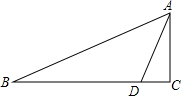 “学数学”最终是为了“用数学”,我市纪台一中校园内有一文物古迹-古纪国点将台,九年级数学兴趣小组想用所学知识测量出点将台的现在高度,操作方案如下:在地面B处测得其顶部A的仰角为30°,自B处沿BC方向进行14m到D点,又测得其顶部A的仰角为60°,你能算出点将台的高度吗?(结果保留两位小数)
“学数学”最终是为了“用数学”,我市纪台一中校园内有一文物古迹-古纪国点将台,九年级数学兴趣小组想用所学知识测量出点将台的现在高度,操作方案如下:在地面B处测得其顶部A的仰角为30°,自B处沿BC方向进行14m到D点,又测得其顶部A的仰角为60°,你能算出点将台的高度吗?(结果保留两位小数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com