
����Ŀ��Ϊ���˽�¸߶�����������״��,ij�����Ը߶��꼶����������(��λ: ![]() )�����˳�������,�õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.��֪������
)�����˳�������,�õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.��֪������![]() ֮�������������������
֮�������������������![]() ֮���������1��.
֮���������1��.

(1)��������![]() ���ڵĶ���Ϊ��������,���õ������и߶�����18000��,��õ����߶����������������Ĵ�Լ�ж�����?
���ڵĶ���Ϊ��������,���õ������и߶�����18000��,��õ����߶����������������Ĵ�Լ�ж�����?
(2)������ȡ��������������![]() ��
��![]() �������������ѡ��2�˵�����ƽʱ��������ϰ�߶����ߵ�Ӱ��,����ѡ����2����������һ�����ߴ���185
�������������ѡ��2�˵�����ƽʱ��������ϰ�߶����ߵ�Ӱ��,����ѡ����2����������һ�����ߴ���185![]() �ĸ����Ƕ���?
�ĸ����Ƕ���?
���𰸡�(1)12600��(2) ![]() .
.
��������
��1����Ƶ�ʷֲ�ֱ��ͼ֪������������Ƶ�ʣ����ǿɵô𰸣�
��2���ȼ�����������������ҳ�������������![]() �е��������Ӷ����ùŵ����ʽ�õ���.
�е��������Ӷ����ùŵ����ʽ�õ���.
��1����Ƶ�ʷֲ�ֱ��ͼ֪������������Ƶ��Ϊ0.7�����Թ������壬���õ������и߶��꼶����������������Ƶ��Ϊ0.7�����Ըõ����߶����������������Ĵ�Լ��![]() ��.
��.
��2��������ȡ������������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ����֪������
����֪������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ����������������
����������������![]() �е���3�ˣ���Ϊ
�е���3�ˣ���Ϊ![]() ��������
��������![]() �е���2�ˣ���Ϊ
�е���2�ˣ���Ϊ![]() ������5������ѡ2�ˣ�����
������5������ѡ2�ˣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() 10�ֲ�ͬ��ѡ��������ÿ��ѡ�����ǻ����ҵȿ��ܵģ����ԣ���ѡ2����������һ�����ߴ���185
10�ֲ�ͬ��ѡ��������ÿ��ѡ�����ǻ����ҵȿ��ܵģ����ԣ���ѡ2����������һ�����ߴ���185![]() �ĸ���
�ĸ���![]() .
.


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ϵ�ļ�����ֱ������ϵ��ԭ���غϣ�������x��ķǸ������غϣ�������C1�ķ���Ϊ��sin����+ ![]() ��+2
��+2 ![]() =0������C2�IJ�������Ϊ
=0������C2�IJ�������Ϊ ![]() ����Ϊ��������
������������
��1����C1�ķ��̻�Ϊֱ�����귽�̣�
��2������QΪC2�ϵĶ��㣬PΪC1�ϵĶ��㣬��|PQ|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㾭���ǹ�Ԫ5�����й��Ŵ����ݷḻ����ѧ���������о��ϵڶ�ʮ���ʣ�������Ů��֯�����湦��������֯��ߣ���һ��֯��ƥ���ɣ������漸�Σ�������˼Ϊ���и�Ů��֯����ÿ���ǰһ���֯��ͬ���IJ�����һ��֯��ߣ�һ���£���30��ƣ���֯390�ߣ��ʣ�ÿ���֯���ٲ�������֪1ƥ=4�ɣ�1��=10�ߣ������ÿ���֯�IJ��IJ�Լ�У� ��
A.0.55��
B.0.53��
C.0.52��
D.0.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ͼ��
��ͼ��![]() ��
��![]() ���㣬��ͼ��ʾ���Һ���
���㣬��ͼ��ʾ���Һ���![]() ��ֵ��Ϊ
��ֵ��Ϊ![]() .���ú���ͼ���ϵĶ���
.���ú���ͼ���ϵĶ���![]() ��
��![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ������
������![]() .
.
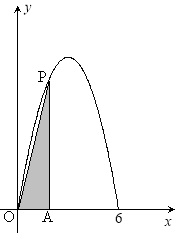
��I��������![]() ������ʽ��
������ʽ��
��������![]() �����Ϊ
�����Ϊ![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|x+m|��
���� �����m�IJ���ʽf��1��+f����2����5��
����x��0ʱ��֤���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx+1��
����֤������x��0ʱ��f��x����x��
������ ![]() ����g��x����0��x��0���������ʵ��a��ȡֵ��Χ��
����g��x����0��x��0���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ����
���� �����ڸ�����������
�����ڸ�����������![]() ��������
��������![]() ����ֵΪ1����Ϊ
����ֵΪ1����Ϊ![]() �����Ƕ���
�����Ƕ���![]() ����
����![]() _____���輯��
_____���輯��![]() ����
����![]() ������Ԫ�صĺ�Ϊ_____��
������Ԫ�صĺ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ�ij���������ȡ���ָ߶�ѧ��,�����䵽У�����ʱ��(��λ:����),�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ(��ͼ),���е�У����ʱ��ķ�Χ��![]() ,�������ݷ���Ϊ
,�������ݷ���Ϊ![]() .
.

(1)��ֱ��ͼ��![]() ��ֵ��
��ֵ��
(2)���ѧ����У����ʱ�䲻����1Сʱ,���������ѧУס��.����У¼ȡ1200������,����Ƹ߶��������ж����˿�������ס�ޣ�
(3)��ֱ��ͼ�е�Ƶ����Ϊ����,�ִӸ�ѧУ�ĸ߶���������ѡ4��ѧ��,��![]() ��ʾ��ѡ4��ѧ���С���У����ʱ������40���ӡ�������,��
��ʾ��ѡ4��ѧ���С���У����ʱ������40���ӡ�������,��![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����գ�x��= ![]() ��a��0
��a��0
��1��������f��x��=lnx+�գ�x�����ڣ�1��2����ֻ��һ����ֵ�㣬��a��ȡֵ��Χ��
��2����g��x��=|lnx|+�գ�x�����Ҷ�����x1 �� x2�ʣ�0��2]����x1��x2 �� ���� ![]() ����1����a��ȡֵ��Χ��
����1����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com