
����Ŀ����ƽ��ֱ������ϵ![]() �У����ڵ�
�У����ڵ�![]() ��ֱ��
��ֱ��![]() �����dz�
�����dz�![]() ��
Ϊ��![]() ��ֱ��
��ֱ��![]() �ķ������.
�ķ������.
��1������Բ![]() �ϵ�����һ��
�ϵ�����һ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ķ������ֱ�Ϊ
�ķ������ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2�����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ķ������ֱ�Ϊ
�ķ������ֱ�Ϊ![]() ��
��![]() �������Ƿ����ʵ��
�������Ƿ����ʵ��![]() ���������
���������![]() ����
����![]() �����������ڣ����
�����������ڣ����![]() ��ֵ�������ڣ�˵������.
��ֵ�������ڣ�˵������.
��3����ֱ֪��![]() ����Բ
����Բ![]() ������Բ
������Բ![]() ����������
����������![]() ��
��![]() ��ֱ��
��ֱ��![]() �ķ������ֱ�Ϊ
�ķ������ֱ�Ϊ![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ���ԱȽ�
���ԱȽ�![]() �ij���
�ij���![]() �Ĵ�С.
�Ĵ�С.
���𰸡���1��![]() ��2������ʵ��
��2������ʵ��![]() ��
��![]() ��3��
��3��![]()
��������
��1��������![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ��������
��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2��������![]() ��
��![]() ������
������![]() ���ɵ�
���ɵ�![]() �������
�������![]() �����������ɵó����ۣ�
�����������ɵó����ۣ�
��3��ȷ��![]() ��
��![]() ��
��![]() ��
��![]() �����ɱȽ�
�����ɱȽ�![]() �ij���
�ij���![]() �Ĵ�С.
�Ĵ�С.
��1���ɵ�![]() ����Բ
����Բ![]() �ϣ�����
�ϣ�����![]()
������![]() ��
��![]() ������
������![]()
��![]() ��
��![]() ����
����![]()
��2���������ʵ��![]() ���������裬
���������裬
������![]() ��
��![]() ��
��
����![]()
![]() �������
�������![]() ������
������
ֻҪ![]() ���ɣ�����
���ɣ�����![]()
�ʴ���ʵ��![]() ��
��![]() ���������
���������![]() ����
����![]() ����.
����.
��3����![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ������
������![]()
![]() ��
��![]() ����
����![]()
��![]() ��
��![]() ��
��![]()
����![]()
����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����![]() ʱ������
ʱ������![]() ��
��
��1����![]() �ı���ʽ��
�ı���ʽ��
��2���費��ʽ![]() ��
��![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���г�����һ�����͵�ǿ��ϴ�·ۣ��ص���ȥ���ٶȿ죬��֪ÿͶ��![]() ��
��![]() ��
��![]() ������λ��ϴ�·�Һ��һ����ˮ��ϴ�»��У�����ˮ���ͷŵ�Ũ��
������λ��ϴ�·�Һ��һ����ˮ��ϴ�»��У�����ˮ���ͷŵ�Ũ��![]() ����/��������ʱ��
����/��������ʱ��![]() �����ӣ��仯�ĺ�����ϵʽ����Ϊ
�����ӣ��仯�ĺ�����ϵʽ����Ϊ![]() ������
������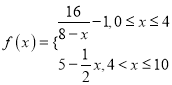 �������Ͷ�ţ���ijһʱ��ˮ�е�ϴ��ҺŨ��Ϊÿ��Ͷ�ŵ�ϴ��Һ����Ӧʱ�����ͷŵ�Ũ��֮�ͣ����ݾ��飬��ˮ��ϴ��Һ��Ũ�Ȳ�����4����/����ʱ������������Чȥ�۵�����.
�������Ͷ�ţ���ijһʱ��ˮ�е�ϴ��ҺŨ��Ϊÿ��Ͷ�ŵ�ϴ��Һ����Ӧʱ�����ͷŵ�Ũ��֮�ͣ����ݾ��飬��ˮ��ϴ��Һ��Ũ�Ȳ�����4����/����ʱ������������Чȥ�۵�����.
��1����ֻͶ��һ��4����λ��ϴ��Һ������Чȥ��ʱ����ܴX���ӣ�
��2������Ͷ��2����λ��ϴ��Һ��6���Ӻ�Ͷ��![]() ����λ��ϴ��Һ��Ҫʹ��������4�������ܹ�������Чȥ�ۣ�����
����λ��ϴ��Һ��Ҫʹ��������4�������ܹ�������Чȥ�ۣ�����![]() ����Сֵ����ȷ��0.1���ο����ݣ�
����Сֵ����ȷ��0.1���ο����ݣ� ![]() ȡ
ȡ![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫����![]() ����֧�ϵ�һ��P��һֱ��l���������߽���A��B���㣬����P��
����֧�ϵ�һ��P��һֱ��l���������߽���A��B���㣬����P��![]() ���е㣻
���е㣻
��1����˫���ߵĽ����߷��̣�
��2����P����Ϊ![]() ʱ����ֱ��l�ķ��̣�
ʱ����ֱ��l�ķ��̣�
��3����֤��![]() ��һ����ֵ��
��һ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У���
����![]() ������������
������������![]() ��
��![]() �����
�����![]() ��D-������.
��D-������.
(1) �ٳ�һ��ǰ�������Ϊ�����D-������(ֻҪ������д�������е�ǰ����)��
(2) ����D-������![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() �������
��д������![]() ��ͨ�ʽ�����ֱ��жϵ�
��ͨ�ʽ�����ֱ��жϵ�![]() ʱ��
ʱ��![]() ��
��![]() �ļ����Ƿ���ڣ�������ڣ�����伫��ֵ(�������ڲ���Ҫ��������)��
�ļ����Ƿ���ڣ�������ڣ�����伫��ֵ(�������ڲ���Ҫ��������)��
(3) ֤��: ����D-������![]() �е������Ϊ
�е������Ϊ![]() ��֤��:
��֤��: ![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ǰ
ǰ![]() ���Ϊ
���Ϊ![]()
(1)������![]() ,�Ҷ��������������
,�Ҷ��������������![]() ����
����![]() ,(����
,(����![]() Ϊ��ʵ����),���������
Ϊ��ʵ����),���������![]() ��ͨ�ʽ.
��ͨ�ʽ.
(2)������![]() �ǵȱ�����,����Ϊ
�ǵȱ�����,����Ϊ![]() ,����Ϊ
,����Ϊ![]() ,
,![]() Ϊ��������ʵ��,����:��
Ϊ��������ʵ��,����:��![]() ,��
,��![]() �ڶ������������
�ڶ������������![]() ,����
,����![]() ;������
;������![]() �����ֵ(��
�����ֵ(��![]() ��
��![]() ��ʾ)
��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() Ϊʵ��������
Ϊʵ��������![]() ��
��
��1��������![]() ��ż��������ʵ��
��ż��������ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ����Сֵ��
����Сֵ��
��3�����ں���![]() ���ڶ������ڸ�������
���ڶ������ڸ�������![]() ���������
���������![]() ������
������![]() ����ƺ���
����ƺ���![]() ������
������![]() �ϵ���ƽ��ֵ��������
�ϵ���ƽ��ֵ��������![]() ������һ������ֵ�������纯��
������һ������ֵ�������纯��![]() ��
��![]() �ϵ�ƽ��ֵ������
�ϵ�ƽ��ֵ������![]() �������ľ�ֵ�㣮���к���
�������ľ�ֵ�㣮���к���![]() ������
������![]() �ϵ�ƽ��ֵ��������ʵ��
�ϵ�ƽ��ֵ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����|x��a|+|x+1|��a��R����g��x����|2x��1|+2.
��1����a��1��֤��������ʽf��x����g��x���������x��R������
��2�����������m��R������t��R��ʹ��f��m����g��t����������ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������
������![]() �붨ֱ��
�붨ֱ��![]() �ľ���֮��Ϊ4.
�ľ���֮��Ϊ4.
��1�����![]() �Ĺ켣���̣����������̵����߲�ͼ��
�Ĺ켣���̣����������̵����߲�ͼ��
��2���ǣ�1���õ��Ĺ켣Ϊ����![]() ��������
��������![]() �Ϲ��ڵ�
�Ϲ��ڵ�![]() ��
��![]() ���ԳƵIJ�ͬ���м��ԣ���˵������.
���ԳƵIJ�ͬ���м��ԣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com