
【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0,另一边CD所在直线方程为x+3y+7=0,
(Ⅰ)求正方形中心G所在的直线方程;
(Ⅱ)设正方形中心G(x0 , y0),当正方形仅有两个顶点在第一象限时,求x0的取值范围.
【答案】解:(Ⅰ)由于正方形中心G所在直线平行于直线x+3y﹣5=0,
设中心所在直线为x+3y+c=0,
由平行线间的距离公式得 ![]() =
= ![]() .
.
解得c=1.
则正方形中心G所在的直线方程为x+3y+1=0;
(Ⅱ)由平行线间的距离公式得正方形的边长为d= ![]() =
= ![]() .
.
设正方形BC,AD所在直线方程为3x﹣y+m=0,
由于中心G(x0 , y0)到BC的距离等于 ![]() =
= ![]() ,
,
那么 ![]() =
= ![]() ,
,
解得m=±6﹣3x0+y0 ①,
又因为G在直线x+3y+1=0上,那么x0+3y0+1=0,即y0=﹣ ![]() ②,
②,
把②代入①得m=±6﹣ ![]() ③,
③,
联立方程 ![]() ,
,
解得 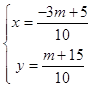 .
.
由于正方形只有两个点在第一象限,那么 ![]() ,
,
就是  ,
,
解得﹣15<m< ![]() ⑤,
⑤,
把③代入⑤得到﹣15<±6﹣ ![]() <
< ![]() ,
,
解得 ![]() <x0<
<x0< ![]() .
.
故x0的取值范围为 ![]()
【解析】(Ⅰ)设中心所在直线为x+3y+c=0,结合正方形的性质和平行线间的距离公式求得c的值;(Ⅱ)由平行线间的距离公式得正方形的边长.设正方形BC,AD所方程为3x﹣y+m=0,联立点G所在直线x0+3y0+1=0,得到 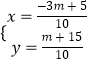 .结合限制性条件正方形仅有两个顶点在第一象限,得到﹣15<m<
.结合限制性条件正方形仅有两个顶点在第一象限,得到﹣15<m< ![]() ,易求x0的取值范围为
,易求x0的取值范围为 ![]() .
.
【考点精析】本题主要考查了两平行线的距离的相关知识点,需要掌握已知两条平行线直线![]() 和
和![]() 的一般式方程为
的一般式方程为![]() :
:![]() ,
,![]()
![]() ,则
,则![]() 与
与![]() 的距离为
的距离为 才能正确解答此题.
才能正确解答此题.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是 ![]() .
. 
(1)求φ;
(2)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(3)求函数f(x)≥1(x∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率. 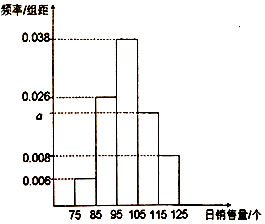
(1)求a的值并估计在一个月(按30天算)内日销售量不低于105个的天数;
(2)利用频率分布直方图估计每天销售量的平均值及方差(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在静水中游泳,速度为4![]() 公里/小时,他在水流速度为4公里/小时的河中游泳.
公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数 ![]() 的导函数
的导函数 ![]() 的图象,对此图象,有如下结论:
的图象,对此图象,有如下结论:
①在区间(-2,1)内 ![]() 是增函数;
是增函数;
②在区间(1,3)内 ![]() 是减函数;
是减函数;
③在 ![]() 时,
时, ![]() 取得极大值;
取得极大值;
④在 ![]() 时,
时, ![]() 取得极小值。
取得极小值。
其中正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com