
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
【答案】(1)见解析;(2)![]() ;(3)63.
;(3)63.
【解析】
(1)直接利用定义求出数列为间等差数列.
(2)利用分类讨论思想,利用数列的前n项和公式求出数列的和,进一步利用不等量关系求出结果.
(3)利用分类讨论思想,进一步求出数列的通项公式,再利用函数的单调性求出k的最大值.
(1)若数列{an}满足an+an+1=2n﹣35,n∈N*,则:an+1+an+2=2(n+1)﹣35,
两式相减得:an+2﹣an=2.故数列{an}是“间等差数列”,公差d=2.
(2)(i)当n=2k时,
![]() (a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=
(a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=![]()
易知:当n=18时,最小值S18=﹣153.
(ii)当n=2k+1时,
Sn=a1+(a2+a3)+(a4+a5)+…+(an﹣1+an)=a1+(﹣31)+(﹣29)+…+(2n﹣37)=![]() ,
,
当n=17时最小,其最小值为S17=a﹣136,要使其最小值为﹣153,
则:a﹣136≥﹣153,解得:a≥﹣17.
(3)易知:cncn+1=2018(![]() )n﹣1,则:cn+1cn+2=2018(
)n﹣1,则:cn+1cn+2=2018(![]() )n,
)n,
两式相除得:![]() ,故数列{cn}为“间等比数列”,其间等比为
,故数列{cn}为“间等比数列”,其间等比为![]() .
.![]() ,
,
易求出数列的通项公式为: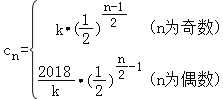 ,
,
由于![]() n>
n>![]() n+1,则数列{
n+1,则数列{![]() n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
要使数列为单调递减数列.只需![]() 2m﹣1>
2m﹣1>![]() 2m>
2m>![]() 2m+1,
2m+1,
即:![]() ,
,
解得![]() ,即最大的整数
,即最大的整数![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
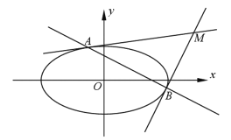
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作两条相异直线分别与圆
作两条相异直线分别与圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 、
、![]() 的倾斜角互补,问直线
的倾斜角互补,问直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() .
.
(1)当![]() 时,试确定曲线
时,试确定曲线![]() 的形状及其焦点坐标;
的形状及其焦点坐标;
(2)若直线![]() 交曲线
交曲线![]() 于点
于点![]() 、
、![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,试问此时曲线
,试问此时曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?
对称?
(3)当![]() 为大于1的常数时,设
为大于1的常数时,设![]() 是曲线
是曲线![]() 上的一点,过点
上的一点,过点![]() 作一条斜率为
作一条斜率为![]() 的直线
的直线![]() ,又设
,又设![]() 为原点到直线
为原点到直线![]() 的距离,
的距离,![]() 分别为点
分别为点![]() 与曲线
与曲线![]() 两焦点的距离,求证
两焦点的距离,求证![]() 是一个定值,并求出该定值.
是一个定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)已知直线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数,且
为参数,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 沿对角线
沿对角线![]() 折成直二面角,下列结论:①异面直线
折成直二面角,下列结论:①异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④二面角
是等边三角形;④二面角![]() 的平面角正切值是
的平面角正切值是![]() ;其中正确结论是______.(写出你认为正确的所有结论的序号)
;其中正确结论是______.(写出你认为正确的所有结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,在
,在![]() 轴截得的弦长为2.
轴截得的弦长为2.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)若![]() 为轨迹
为轨迹![]() 上一动点,过点
上一动点,过点![]() 作圆
作圆![]() 的两条切线分别交
的两条切线分别交![]() 轴于
轴于![]() ,
,![]() 两点,求
两点,求![]() 面积的最小值,并求出此时点
面积的最小值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com