
【题目】已知曲线![]() 的方程为
的方程为![]() .
.
(1)当![]() 时,试确定曲线
时,试确定曲线![]() 的形状及其焦点坐标;
的形状及其焦点坐标;
(2)若直线![]() 交曲线
交曲线![]() 于点
于点![]() 、
、![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,试问此时曲线
,试问此时曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?
对称?
(3)当![]() 为大于1的常数时,设
为大于1的常数时,设![]() 是曲线
是曲线![]() 上的一点,过点
上的一点,过点![]() 作一条斜率为
作一条斜率为![]() 的直线
的直线![]() ,又设
,又设![]() 为原点到直线
为原点到直线![]() 的距离,
的距离,![]() 分别为点
分别为点![]() 与曲线
与曲线![]() 两焦点的距离,求证
两焦点的距离,求证![]() 是一个定值,并求出该定值.
是一个定值,并求出该定值.
【答案】(1) 曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,焦点坐标为
轴上的椭圆,焦点坐标为![]() ; (2) 见解析;(3)见证明
; (2) 见解析;(3)见证明
【解析】
(1)将a代入,两边平方并化简,可得曲线C的方程及形状;
(2)将![]() 代入曲线,利用PQ中点的横坐标为
代入曲线,利用PQ中点的横坐标为![]() ,求出m,验证判别式是否成立,可得结论.
,求出m,验证判别式是否成立,可得结论.
(3)将曲线C化简,得到焦点坐标,求得![]() ,再求得点到直线
,再求得点到直线![]() 的距离,代入
的距离,代入![]() 化简得到定值.
化简得到定值.
(1)当![]() 时,
时,![]() ,两边平方并化简得
,两边平方并化简得![]() ,
,
∴曲线![]() 是焦点在
是焦点在![]() 轴上的椭圆,其长半轴长为1,短半轴长为
轴上的椭圆,其长半轴长为1,短半轴长为![]() ,焦点坐标为
,焦点坐标为![]() ;
;
(2)将![]() 代入
代入![]() ,消去
,消去![]() ,
,
得![]() ,由题意,
,由题意,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),此时,
(舍),此时,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,则
,则 ,
,
![]() 的中点坐标为
的中点坐标为![]() 在对称轴
在对称轴![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
,
不满足![]() ,∴曲线
,∴曲线![]() 上不存在不同的两点
上不存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称;
对称;
(3)![]() ,两焦点坐标为
,两焦点坐标为![]() 、
、![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴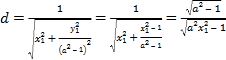 ,
,
用![]() 替换
替换![]() 中的
中的![]() ,
,
可得![]() ,∴
,∴![]() ,
,
∴![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于![]() 的偶数可以表示为两个素数的和”,如
的偶数可以表示为两个素数的和”,如![]() .现从不超过
.现从不超过![]() 的素数中,随机选取两个不同的数(两个数无序).(注:不超过
的素数中,随机选取两个不同的数(两个数无序).(注:不超过![]() 的素数有
的素数有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)列举出满足条件的所有基本事件;
(2)求“选取的两个数之和等于![]() ”事件发生的概率.
”事件发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。

(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com