
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() ,现从数列
,现从数列![]() 的前2020项中随机抽取1项,则该项不能被3整除的概率是( )
的前2020项中随机抽取1项,则该项不能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
这是一个古典概型,总的基本事件数是2020,根据![]() ,
,![]() ,可得数列的项依次为1,1,2,3,5,8,13,21,34,55,89,144,……,由整除的定义可得第一项被3整除的余数为1,第二项被3整除的余数为1,则第三项被3整除的余数为2,故其第四项可以被3整除,依此分析可知数列中第4n项(
,可得数列的项依次为1,1,2,3,5,8,13,21,34,55,89,144,……,由整除的定义可得第一项被3整除的余数为1,第二项被3整除的余数为1,则第三项被3整除的余数为2,故其第四项可以被3整除,依此分析可知数列中第4n项(![]() 且
且![]() )可以被3整除,得到基本事件数,利用概率公式可得整除的概率,然后用对立事件的概率求得不能被整除的概率.
)可以被3整除,得到基本事件数,利用概率公式可得整除的概率,然后用对立事件的概率求得不能被整除的概率.
根据题意,数列的项依次为1,1,2,3,5,8,13,21,34,55,89,144,……,
则第一项被3整除的余数为1,第二项被3整除的余数为1,则第三项被3整除的余数为2,故其第四项可以被3整除.
同理,第五项被3整除的余数为1,第六项被3整除的余数为1,则第七项被3整除的余数为2,故其第八项可以被3整除.
依此类推,分析可得数列中第4n项(![]() 且
且![]() )可以被3整除.
)可以被3整除.
数列的前2020项中,有505项可以被3整数,
故从数列的前2020项中随机抽取1项,不能被3整除的概率![]() ;
;
故选:D.


科目:高中数学 来源: 题型:
【题目】某公司以客户满意为出发点,随机抽选2000名客户,以调查问卷的形式分析影响客户满意度的各项因素.每名客户填写一个因素,下图为客户满意度分析的帕累托图.帕累托图用双直角坐标系表示,左边纵坐标表示频数,右边纵坐标表示频率,分析线表示累计频率,横坐标表示影响满意度的各项因素,按影响程度(即频数)的大小从左到右排列,以下结论正确的个数是( ).
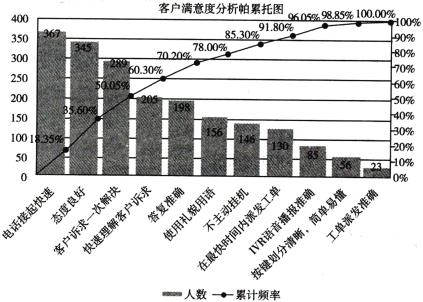
①35.6%的客户认为态度良好影响他们的满意度;
②156位客户认为使用礼貌用语影响他们的满意度;
③最影响客户满意度的因素是电话接起快速;
④不超过10%的客户认为工单派发准确影响他们的满意度.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,E,M分别是BC,PD中点,点F在棱PC上移动.
,E,M分别是BC,PD中点,点F在棱PC上移动.
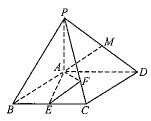
(1)证明无论点F在PC上如何移动,都有平面![]() 平面
平面![]() ;
;
(2)当直线AF与平面PCD所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学与文学之间存在着奇妙的联系,诗中有回文诗,如“山东落花生花落东山,西湖回游鱼游回湖西”,倒过来读,仍然是原句!数学上也有这样一类数,如66,202,3773,34543,无论从左往右读,还是从右往左读,都是同一个数,我们称这样的数为“回文数”,现用数字1,2,3,4组数(可重复用),则组成的五位“回文数”的个数为( )
A.24B.28C.48D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为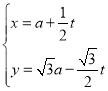 (t为参数,
(t为参数,![]() ).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点![]() 在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
(2)已知![]() ,点P在直线l上,点Q在曲线C上,且
,点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两同学参加数学竞赛培训,在培训期间,他们参加了8次测验,成绩(单位:分)记录如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7![]() 8
8![]() 76 85
76 85
B同学的成绩不慎被墨迹污染(![]() ,
,![]() 分别用m,n表示).
分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A、B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请说明理由(不用计算);
(2)若B同学的平均分为78,方差![]() ,求m,n.
,求m,n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com