
【题目】如图,在四棱锥P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E为AD的中点,AC与BE相交于点O.
,E为AD的中点,AC与BE相交于点O.
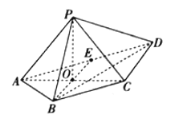
(1)证明:![]() 平面ABCD.
平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]() 焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
(1)证明:点M在一条定直线上;
(2)记点M所在定直线为l,与y轴交于点N,MF与抛物线C交于P,Q两点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为2.
上的点到准线的最小距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 分别为弦
分别为弦![]() ,
,![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率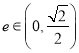 ,
,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 为椭圆的上、下顶点,且
为椭圆的上、下顶点,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,证明:在第一象限内存在定点
两点,证明:在第一象限内存在定点![]() ,使得当直线
,使得当直线![]() 与直线
与直线![]() 的斜率均存在时,其斜率之和是与
的斜率均存在时,其斜率之和是与![]() 无关的常数,并求出所有满足条件的定点
无关的常数,并求出所有满足条件的定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种掷骰子走跳棋的游戏:棋盘上标有第0站、第1站、第2站、…、第100站,共101站,设棋子跳到第n站的概率为![]() ,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
,一枚棋子开始在第0站,棋手每掷一次骰子,棋子向前跳动一次.若掷出奇数点,棋子向前跳一站;若掷出偶数点,棋子向前跳两站,直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具,它的六个面分别标有点数1,2,3,4,5,6).
(1)求![]() ,
,![]() ,
,![]() ,并根据棋子跳到第n站的情况,试用
,并根据棋子跳到第n站的情况,试用![]() 和
和![]() 表示
表示![]() ;
;
(2)求证:![]() 为等比数列;
为等比数列;
(3)求玩该游戏获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医院为筛查某种疾病,需要血检,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,需要检验![]() 次;
次;
方式二:混合检验,把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这
个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这![]() 个人只作一次检验就够了;如果结果是阳性,那么再对这
个人只作一次检验就够了;如果结果是阳性,那么再对这![]() 个人的另一份血样逐份检验,此时这
个人的另一份血样逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.
次.
(1)假设有6份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验岀来的概率;
(2)假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是双曲线
是双曲线![]() 的左右焦点,以
的左右焦点,以![]() 为直径的圆与双曲线的一条渐近线交于点
为直径的圆与双曲线的一条渐近线交于点![]() ,与双曲线交于点
,与双曲线交于点![]() ,且
,且![]() 均在第一象限,当直线
均在第一象限,当直线![]() 时,双曲线的离心率为
时,双曲线的离心率为![]() ,若函数
,若函数![]() ,则
,则![]() ()
()
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为1,
的面积为1,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 、
、![]() 是椭圆的左右两个焦点,直线
是椭圆的左右两个焦点,直线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com