练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知cos = ，cos cos = ，cos cos cos = ，…，根据这些结果，猜想出的一般结论是 ．

    【答案】cos cos …cos =
    【解析】解：根据题意，分析所给的等式可得： cos = ，可化为cos =
    cos cos = ，可化为cos cos =
    cos cos cos = ，可化为cos cos cos = ；
    则一般的结论为cos cos …cos = ；
    所以答案是cos cos …cos = ．
    【考点精析】认真审题，首先需要了解归纳推理(根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知命题P：4x﹣a2x+1≥0对x∈[﹣1，1]恒成立，命题Q：f（x）=log2（ax2﹣2x+ ）的值域是R，若满足P且Q为假，P或Q为真，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连接EC、CD．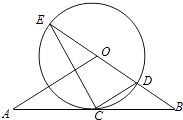

    （1）求证：直线AB是⊙O的切线；
    （2）若tan∠CED= ，⊙O的半径为3，求OA的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据要求，解答下列问题。
    （1）求经过点A（3，2），B（-2，0）的直线方程；
    （2）求过点P(-1，3),并且在两轴上的截距相等的直线方程；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1 ． 求证：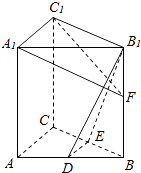

    （1）直线DE∥平面A1C1F；
    （2）平面B1DE⊥平面A1C1F．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的倾斜角 的余弦值 ，则此直线的斜率是（ ）．
    A.
    B.－
    C.
    D.±

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程选讲

    以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，

    在直角坐标系中，曲线的参数方程为（是参数， ），以原点为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）当时，曲线和相交于、两点，求以线段为直径的圆的直角坐标方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

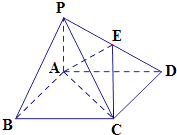
    【题目】如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，AP=1，AD=2，E为线段PD上一点，记 =λ． 当λ= 时，二面角D﹣AE﹣C的平面角的余弦值为 ．

    （1）求AB的长；
    （2）当 时，求异面直线BP与直线CE所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第12界全运会于2013年8月31日在辽宁沈阳顺利举行，组委会在沈阳某大学招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位： ），身高在175以上（包括175）定义为“高个子”，身高在175以下（不包括175）定义为“非高个子”.

    （1）如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率？

    （2）若从身高180以上（包括180）的志愿者中选出男、女各一人，求这两人身高相差5以上的概率．

    查看答案和解析>>

    同步练习册答案