
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线![]() 的参数方程为
的参数方程为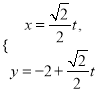 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为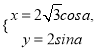 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和
和![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若![]() 为曲线
为曲线![]() 上的一个动点,求
上的一个动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下的2×2列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可能性要求,能否认为“成绩与班级有关系”?
P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式及数据:K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),直线
),直线![]() 与抛物线
与抛物线![]() 交于
交于![]() (点
(点![]() 在点
在点![]() 的左侧)两点,且
的左侧)两点,且![]() .
.
(1)求抛物线![]() 在
在![]() 两点处的切线方程;
两点处的切线方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且
两点,且![]() 的中点在线段
的中点在线段![]() 上,
上, ![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 是圆
是圆![]() :
: ![]() 上的任意一点,点
上的任意一点,点![]() 与点
与点![]() 的连线段的垂直平分线和
的连线段的垂直平分线和![]() 相交于点
相交于点![]() .
.
(I)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(II)过坐标原点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于点
于点![]() ,
, ![]() 两点,直线
两点,直线![]() 与坐标轴不重合.
与坐标轴不重合. ![]() 是轨迹
是轨迹![]() 上的一点,若
上的一点,若![]() 的面积是4,试问直线
的面积是4,试问直线![]() ,
, ![]() 的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
的斜率之积是否为定值,若是,求出此定值,否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com