练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温（单位； ）的数据，绘制了下面的折线图。

    已知该市的各月最低气温与最高气温具有较好的线性关系，则根据该折线图，下列结论错误的是（ ）
    A.最低气温与最高气温为正相关
    B.10月的最高气温不低于5月的最高气温
    C.月温差（最高气温减最低气温）的最大值出现在1月
    D.最低气温低于 的月份有4个

    【答案】D
    【解析】由图可以看出，当最低气温较大时，最高气温也较大，故A正确；10月份的最高气温大于20 ，而5月份的最高气温为不超过20 ，故B正确；从各月的温差看，1月份的温差最大，故C正确；而最低气温低于 的月份是1，2，4三月份，故D错，所以答案是：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ex－e－x(x∈R，且e为自然对数的底数).
    （1）判断函数f(x)的单调性与奇偶性；
    （2）是否存在实数t ， 使不等式f(x－t)＋f(x2－t2)≥0对一切x∈R都成立？若存在，求出t；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某人到甲、乙两市各 个小区调查空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为（ ）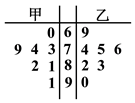

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， 为圆柱 的母线， 是底面圆 的直径， 是 的中点.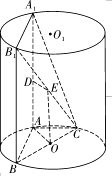

    （Ⅰ）问： 上是否存在点 使得 平面 ？请说明理由；
    （Ⅱ）在（Ⅰ）的条件下，若 平面 ，假设这个圆柱是一个大容器，有条体积可以忽略不计的小鱼能在容器的任意地方游弋，如果小鱼游到四棱锥 外会有被捕的危险，求小鱼被捕的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工厂为预测产品的回收率 ，需要研究它和原料有效成分含量 之间的相关关系，现收集了4组对照数据。

    3

    4

    5

    6

    2.5

    3

    4

    4.5

    （Ⅰ）请根据相关系数 的大小判断回收率 与 之间是否存在高度线性相关关系；
    （Ⅱ）请根据上表提供的数据，用最小二乘法求出 关于 的线性回归方程 ，并预测当 时回收率 的值.
    参考数据：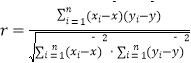

    1

    0

    其他

    相关关系

    完全相关

    不相关

    高度相关

    低度相关

    中度相关

    ，

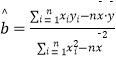    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程
    在直角坐标系 中，直线 的参数方程为 （ 为参数），直线 的参数方程为 （ 为参数），设 与 的交点为 ，当 变化时， 的轨迹为曲线 .
    （1）写出 的普遍方程及参数方程；
    （2）以坐标原点为极点， 轴正半轴为极轴建立极坐标系，设曲线 的极坐标方程为 ， 为曲线 上的动点，求点 到 的距离的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

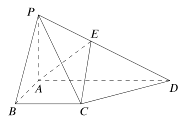
    【题目】如图，在四棱锥 中，底面 为直角梯形， ，且 ， 平面 .

    （1）求 与平面 所成角的正弦值；
    （2）棱 上是否存在一点 满足 ?若存在，求 的长；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于椭圆 ，有如下性质：若点 是椭圆上的点，则椭圆在该点处的切线方程为 .利用此结论解答下列问题.
    （Ⅰ）求椭圆 的标准方程；
    （Ⅱ）若动点 在直线 上，经过点 的直线 与椭圆 相切，切点分别为 .求证直线 必经过一定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，若输出的 值为11，则判断框中的条件可以是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案