[题目]设命题:实数满足.其中.命题:实数满足.(1)若.且为真.求实数的取值范围,(2)若是的充分不必要条件.求实数的取值范围. 题目和参考答案——青夏教育精英家教网—

【题目】设命题：实数满足，其中，命题：实数满足.

（1）若，且为真，求实数的取值范围；

（2）若是的充分不必要条件，求实数的取值范围.

【答案】（1）（2）

【解析】

（1）当时，求得不等式的解集.求得不等式组的解集，根据为真，得到均为真命题，对两个不等式的解集求交集，求得实数的取值范围.（2）由（1）得到不等式组的解集，求得不等式的解集，将“是的充分不必要条件”转化为“是的充分不必要条件”，根据充分不必要条件的知识列不等式组，解不等式组求得的取值范围.

解：（1）由得

又，所以，

当时，不等式的解集为，

即命题为真命题时，实数的范围是

由解得，

即命题为真，则实数的范围为

又为真，所以所求范围为

（2）若是的充分不必要条件是的充分不必要条件

设，，则

∴实数满足，所以实数的取值范围是.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】进入12月以业，在华北地区连续出现两次重污染天气的严峻形势下，我省坚持保民生，保蓝天，各地严格落实机动车限行等一系列“管控令”，某市交通管理部门为了了解市民对“单双号限行”的态度，随机采访了200名市民，将他们的意见和是否拥有私家车的情况进行了统计，得到如下的列联表：

	赞同限行	不赞同限行	合计
没有私家车	90	20	110
有私家车	70	40	110
合计	160	60	220

(1)根据上面的列联表判断能否在犯错误的概率不超过的前提下认为“对限行的态度与是否拥有私家车有关”；

(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用，从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人，再从这6人中随机抽出3名进行电话回访，求3人中至少有1人没有私家车的概率.

附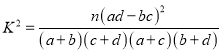：，其中.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】是抛物线为上的一点，以S为圆心，r为半径做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点．

求抛物线的方程．

求证：直线CD的斜率为定值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆：的左、右有顶点分别是、，上顶点是，圆：的圆心到直线的距离是，且椭圆的右焦点与抛物线的焦点重合．

（Ⅰ）求椭圆的方程；

（Ⅱ）平行于轴的动直线与椭圆和圆在第一象限内的交点分别为、，直线、与轴的交点记为，．试判断是否为定值，若是，证明你的结论．若不是，举反例说明．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）求函数的定义域；

（2）若函数的最小值为，求的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《中华人民共和国个人所得税法》第十四条中有下表(部分):

个人所得税税率(工资、薪金所得适用)

级数	全月应纳所得额	税率(%)
1	不超过元的部分
2	超过元至元的部分
3	超过元至元的部分
4	超过元至元的部分
5	超过元至元的部分