
【题目】已知AF![]() 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)AC![]() BC,BE
BC,BE![]() AC,所以AC
AC,所以AC![]() 平面BCE.(2)存在,点M为线段EF中点。
平面BCE.(2)存在,点M为线段EF中点。
试题解析:
(1)过C作CN![]() AB,垂足为N,因为AD
AB,垂足为N,因为AD![]() DC,所以四边形ADCN为矩形.所以AN
DC,所以四边形ADCN为矩形.所以AN![]() NB
NB![]() 2.又因为AD
2.又因为AD![]() 2,AB
2,AB![]() 4,所以AC
4,所以AC![]() ,CN
,CN![]() ,BC
,BC![]() , 所以AC2+BC2
, 所以AC2+BC2![]() AB2,所以AC
AB2,所以AC![]() BC;
BC;
因为AF![]() 平面ABCD,AF//BE所以BE
平面ABCD,AF//BE所以BE![]() 平面ABCD,所以BE
平面ABCD,所以BE![]() AC,
AC,
又因为BE![]() 平面BCE,BC
平面BCE,BC![]() 平面BCE,BE
平面BCE,BE![]() BC
BC![]() B,
B,
所以AC![]() 平面BCE.
平面BCE.

(2)存在,点M为线段EF中点,证明如下:在矩形ABEF中,因为点M,N为线段AB的中点,所以四边形BEMN为正方形,所以BM![]() EN;因为AF
EN;因为AF![]() 平面ABCD,AD
平面ABCD,AD![]() 平面ABCD,所以AF
平面ABCD,所以AF![]() AD.在直角梯形ABCD中,AD
AD.在直角梯形ABCD中,AD![]() AB,又AF
AB,又AF![]() AB
AB![]() A,所以AD
A,所以AD![]() 平面ABEF,又CN//AD,所以CN
平面ABEF,又CN//AD,所以CN![]() 平面ABEF,
平面ABEF,
又BM![]() 平面ABEF所以CN
平面ABEF所以CN![]() BM;
BM;
又 CN![]() EN
EN![]() N,所以BM
N,所以BM![]() 平面ENC,
平面ENC,
又EC![]() 平面ENC,
平面ENC,
所以BM![]() CE.
CE.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,三个点
,三个点![]() ,
, ![]() ,
, ![]() 中恰有两个点在
中恰有两个点在![]() 上.
上.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线交
的直线交![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 为
为![]() 上任意一点,证明:直线
上任意一点,证明:直线![]() ,
, ![]() ,
, ![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】具有性质:![]() 的函数,我们称为满足“倒负”变换的函数。给出下列函数:
的函数,我们称为满足“倒负”变换的函数。给出下列函数:
①![]() ②
②![]() ③
③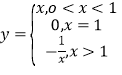 其中满足“倒负”变换的函数是()
其中满足“倒负”变换的函数是()
A. ①② B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AF![]() 平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,
平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若
,若![]() 且
且![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)解不等式![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() ,
, ![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 方程;
方程;
(Ⅱ)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交
相交![]() 两点,试问在
两点,试问在![]() 轴上是否存在与点
轴上是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com