
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线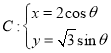 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.4,购买乙种保险但不购买甲种保险的概率为0.2.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲乙两种保险都不购买的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
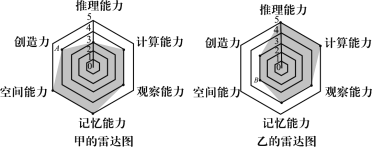
A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点![]() 且倾斜角为
且倾斜角为![]() .以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为
.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() ,l与C交于M,N两点.
,l与C交于M,N两点.
(1)求C的直角坐标方程和![]() 的取值范围;
的取值范围;
(2)求MN中点H的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某种不透明充气包装的袋装零食,每袋零食附赠玩具A,B,C中的一个.对某零售店售出的100袋零食中附赠的玩具类型进行追踪调查,得到以下数据:
BBABC ACABA AAABC BABAA CAAAB
ABCCC BCBBC CABCA BACAB BCBCB
BCCCA BCCAA BCCCB ACCBB BACAB
ACCAB BBBAA CABCA BCBBC CABCA
(1)能否认为购买一袋该零食,获得玩具A,B,C的概率相同?请说明理由;
(2)假设每袋零食随机附赠玩具A,B,C是等可能的,某人一次性购买该零食3袋,求他能从这3袋零食中集齐玩具A,B及C的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
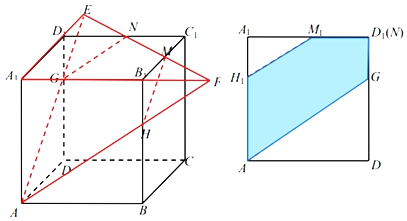
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com