
【题目】已知函数![]() ,
,![]() ,设
,设![]() .
.
(1)如果曲线![]() 与曲线
与曲线![]() 在
在![]() 处的切线平行,求实数
处的切线平行,求实数![]() 的值;
的值;
(2)若对![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 存在极大值与极小值,请比较
存在极大值与极小值,请比较![]() 的极大值与极小值的大小,并说明理由.
的极大值与极小值的大小,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3) 当
;(3) 当![]() 时,
时,![]() 极大值大于极小值;
极大值大于极小值;
当![]() 时,
时,![]() 极大值小于极小值.
极大值小于极小值.
【解析】
(1)分别求出两个函数的导数,把![]() 代入两个导函数中,根据线线平行斜率的关系,可以求出实数
代入两个导函数中,根据线线平行斜率的关系,可以求出实数![]() 的值;
的值;
(2)对函数![]() 求导,分类讨论函数的单调性,最后求出实数
求导,分类讨论函数的单调性,最后求出实数![]() 的取值范围;
的取值范围;
(3)令![]() 的导函数等于零,求题意确定实数
的导函数等于零,求题意确定实数![]() 的取值范围,分类讨论,根据函数的单调性确定极大值与极小值之间的大小关系即可.
的取值范围,分类讨论,根据函数的单调性确定极大值与极小值之间的大小关系即可.
(1)因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]()
(2)![]()
![]() ,
,
易知![]() ,
,
![]()
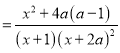
①当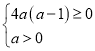 ,即
,即![]() 时,有
时,有![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,满足题意.
,满足题意.
②当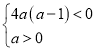 ,即
,即![]() 时,
时,
![]() ,得
,得![]() ,
,![]()
因为![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是减函数,
上是减函数,
![]() ,不符合题意.
,不符合题意.
综上,![]() .
.
(3)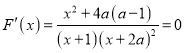 ,
,
即![]() 有两个不相等实数根
有两个不相等实数根![]() ,
,![]()
因为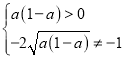 ,
,
所以![]() 且
且![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,
![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
故![]() 极大值为
极大值为![]() ,极小值为
,极小值为![]() ,且
,且![]() .
.
②当![]() 时,即
时,即![]() 时,
时,
![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
故![]() 极大值为
极大值为![]() ,极小值为
,极小值为![]() .
.
![]()
![]()
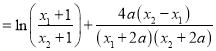 ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
综上,当![]() 时,
时,![]() 极大值大于极小值;
极大值大于极小值;
当![]() 时,
时,![]() 极大值小于极小值.
极大值小于极小值.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 ,第6小组的频数是7 .

(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记![]() 表示两人中进入决赛的人数,求
表示两人中进入决赛的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ) 经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若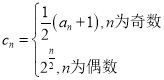
![]() ,从数列
,从数列![]() 中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
中抽出部分项(奇数项与偶数项均不少于两项),将抽出的项按照某一顺序排列后构成等差数列.当等差数列的项数最大时,求所有满足条件的等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃,价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元,顾客就少付x(2x∈Z)元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
①若顾客一次购买松子和腰果各1千克,需要支付180元,则x=________;
②在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且满足:
且满足:![]()
(1)证明:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式.
的通项公式.
(2)设![]() ,若数列
,若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)在(2)的条件下,设![]() 记数列
记数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() 存在实数
存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ,
,![]() 为异面直线; ②若
为异面直线; ②若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ; ④若
; ④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
则上述命题中真命题的序号为( )
A.①②B.③④C.②D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com