
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]()
![]() 分别是椭圆的左右焦点,点
分别是椭圆的左右焦点,点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() .
.
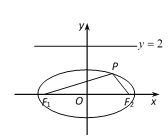
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在直线![]() 上是否存在点Q,使以
上是否存在点Q,使以![]() 为直径的圆经过坐标原点O,若存在,求出线段
为直径的圆经过坐标原点O,若存在,求出线段![]() 的长的最小值,若不存在,请说明理由.
的长的最小值,若不存在,请说明理由.
【答案】(Ⅰ) ![]() . (Ⅱ)存在,最小值是
. (Ⅱ)存在,最小值是![]()
【解析】
(Ⅰ) 根据椭圆的定义可得,![]() ,又离心率
,又离心率![]() ,可以解出
,可以解出![]() ,再根据
,再根据![]() 求出
求出![]() ,即可得到椭圆的标准方程;
,即可得到椭圆的标准方程;
(Ⅱ) 假设在直线![]() 上存在点
上存在点![]() ,则
,则![]() ,即
,即![]() ,根据点
,根据点![]() 如可求出
如可求出![]() 点坐标,即说明存在;根据距离公式可求出
点坐标,即说明存在;根据距离公式可求出![]() ,结合点
,结合点![]() 是椭圆上任意一点可得
是椭圆上任意一点可得![]() ,消去
,消去![]() ,由基本不等式即可求出
,由基本不等式即可求出![]() 的最小值,并求得
的最小值,并求得![]() 点坐标.
点坐标.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
∵点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() .
.
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴所求椭圆的标准方程为![]() .
.
(Ⅱ)假设在直线![]() 上存在点Q,使以
上存在点Q,使以![]() 为直径的圆经过坐标原点O,
为直径的圆经过坐标原点O,
则![]() .∴
.∴![]() .
.

设![]() ,
,![]() ,则
,则![]() .
.![]()
∴![]() .
.
当![]() 时,以
时,以![]() 为直径的圆不经过坐标原点O.
为直径的圆不经过坐标原点O.
当![]() 时,
时,![]() .
.
∴![]()
![]()
![]()
∵点![]() 在椭圆上,∴
在椭圆上,∴![]() .∴
.∴![]() .
.
∴![]()
![]() .
.
![]() ,当且仅当
,当且仅当![]() 或
或![]() 时取等号,此时
时取等号,此时![]() ,
,
所以![]() ,
,![]() 的最小值是
的最小值是![]() .
.
所以,在直线![]() 上存在点
上存在点![]() ,使以
,使以![]() 为直径的圆经过坐标原点O,且线段PQ的长的最小值是
为直径的圆经过坐标原点O,且线段PQ的长的最小值是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的六面体中,四边形![]() 是边长为
是边长为![]() 的正方形,四边形
的正方形,四边形![]() 是梯形,
是梯形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
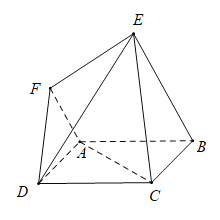
(1)在图中作出平面 ![]() 与平面
与平面![]() 的交线,并写出作图步骤,但不要求证明;
的交线,并写出作图步骤,但不要求证明;
(2)求证:![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以椭圆![]() :
:![]() 的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 交于异于椭圆顶点的
交于异于椭圆顶点的![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() 点,直线
点,直线![]() 和直线
和直线![]() 的斜率之积为1,直线
的斜率之积为1,直线![]() 与
与![]() 轴交于点
轴交于点![]() .若直线
.若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试判断
,试判断![]() 是否为定值,若是,求出该定值;若不是,说明理由.
是否为定值,若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的![]() 城市和交通拥堵严重的
城市和交通拥堵严重的![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小(不要求计算具体值,给出结论即可);
(2)若得分不低于85分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此列联表,并据此样本分析是否有![]() 的把握认为城市拥堵与认可共享单车有关;
的把握认为城市拥堵与认可共享单车有关;
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)若此样本中的![]() 城市和
城市和![]() 城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自
城市各抽取1人,则在此2人中恰有一人认可的条件下,此人来自![]() 城市的概率是多少?
城市的概率是多少?
(参考公式: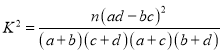 )
)
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机![]() 软件层出不穷.为调查某款订餐软件的商家的服务情况,统计了10次订餐“送达时间”,得到茎叶图如下:(时间:分钟)
软件层出不穷.为调查某款订餐软件的商家的服务情况,统计了10次订餐“送达时间”,得到茎叶图如下:(时间:分钟)
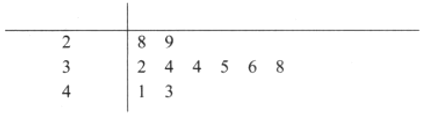
(1)请计算“送达时间”的平均数与方差:
(2)根据茎叶图填写下表:
送达时间 | 35分组以内(包括35分钟) | 超过35分钟 |
频数 | A | B |
频率 | C | D |
在答题卡上写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(3)在(2)的情况下,以频率代替概率.现有3个客户应用此软件订餐,求出在35分钟以内(包括35分钟)收到餐品的人数![]() 的分布列,并求出数学期望.
的分布列,并求出数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的进步与发展,中国的网民数量急剧增加.下表是中国从![]() 年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年网民人数及互联网普及率、手机网民人数(单位:亿)及手机网民普及率的相关数据.
年份 | 网民人数 | 互联网普及率 | 手机网民人数 | 手机网民普及率 |
2009 |
|
|
|
|
2010 |
|
|
|
|
2011 |
|
|
|
|
2012 |
|
|
|
|
2013 |
|
|
|
|
2014 |
|
|
|
|
2015 |
|
|
|
|
2016 |
|
|
|
|
2017 |
|
|
|
|
2018 |
|
|
|
|
(互联网普及率![]() (网民人数/人口总数)×100%;手机网民普及率
(网民人数/人口总数)×100%;手机网民普及率![]() (手机网民人数/人口总数)×100%)
(手机网民人数/人口总数)×100%)
(Ⅰ)从![]() 这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
这十年中随机选取一年,求该年手机网民人数占网民总人数比值超过80%的概率;
(Ⅱ)分别从网民人数超过6亿的年份中任选两年,记![]() 为手机网民普及率超过50%的年数,求
为手机网民普及率超过50%的年数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)若记![]() 年中国网民人数的方差为
年中国网民人数的方差为,手机网民人数的方差为
![]() ,试判断
,试判断![]() 与
与![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票,为了研究网络购票人群的年龄分布情况,在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录,按年龄段将数据分成6组:![]() ,得到如下直方图:
,得到如下直方图:
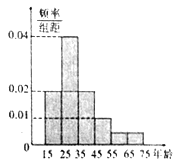
(1)试通过直方图,估计5月31日当天网络购票的9600名乘客年龄的中位数;
(2)若在调查的且年龄在![]() 段乘客中随机抽取两人,求两人均来自同一年龄段的概率.
段乘客中随机抽取两人,求两人均来自同一年龄段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,且该圆经过点
,且该圆经过点![]() .
.
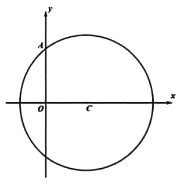
(1)求圆![]() 的标准方程;
的标准方程;
(2)若点![]() 也在圆
也在圆![]() 上,且弦
上,且弦![]() 长为8,求直线
长为8,求直线![]() 的方程;
的方程;
(3)直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率之积为2,求证:直线
的斜率之积为2,求证:直线![]() 过一个定点,并求出该定点坐标.
过一个定点,并求出该定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com