
设向量
 ,定义一种向量积
,定义一种向量积 .
.
已知向量 ,
, ,点
,点 为
为 的图象上的动点,点
的图象上的动点,点 为
为 的图象上的动点,且满足
的图象上的动点,且满足 (其中
(其中 为坐标原点).
为坐标原点).
(1)请用 表示
表示 ;
;
(2)求 的表达式并求它的周期;
的表达式并求它的周期;
(3)把函数 图象上各点的横坐标缩小为原来的
图象上各点的横坐标缩小为原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象.设函数
的图象.设函数

 ,试讨论函数
,试讨论函数 在区间
在区间 内的零点个数.
内的零点个数.
(1)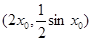 ;(2)
;(2)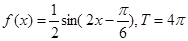 ;(3)当
;(3)当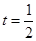 或
或 时,函数
时,函数 在区间
在区间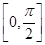 内只有一个零点;当
内只有一个零点;当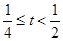 时,函数
时,函数 在区间
在区间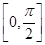 内有两个零点;当
内有两个零点;当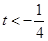 或
或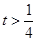 时,函数
时,函数 在区间
在区间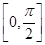 内没有零点.
内没有零点.
解析试题分析:解题思路:(1)利用定义的运算用 表示
表示 即可;(2)根据图像变换得到
即可;(2)根据图像变换得到 的解析式,(3)得出
的解析式,(3)得出 的单调区间,讨论零点个数即可.规律总结:(1)对于新定义题目,要真正理解定义,想法与所学知识联系,是解决新定义题目的关键;(2)讨论零点个数,即讨论图像与
的单调区间,讨论零点个数即可.规律总结:(1)对于新定义题目,要真正理解定义,想法与所学知识联系,是解决新定义题目的关键;(2)讨论零点个数,即讨论图像与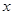 轴的交点个数..
轴的交点个数..
试题解析:(1) ,
,
(2)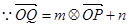 ,
,
 ,即
,即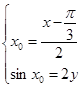 ,
,
所以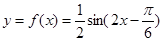 ,它的周期为
,它的周期为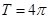 .
.
(3)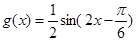 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
又 ,
,
当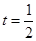 或
或 时,函数
时,函数 在区间
在区间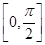 内只有一个零点;当
内只有一个零点;当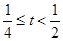 时,函数
时,函数 在区间
在区间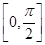 内有两个零点;当
内有两个零点;当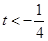 或
或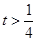 时,函数
时,函数 在区间
在区间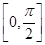 内没有零点.
内没有零点.
考点:新定义型题、三角函数的图像与性质、函数的零点.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com