
【题目】已知椭圆![]() ,过点
,过点![]() 作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
(1)求椭圆C的方程;
(2)F为椭圆C的右焦点,过点F且与x轴不垂直的直线![]() 交椭圆C于A,B两点,点A关于x轴的对称点为
交椭圆C于A,B两点,点A关于x轴的对称点为![]() ,则直线
,则直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() 过定点
过定点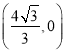 .
.
【解析】
(1)设出直线l的方程,联立直线与椭圆方程,利用相切得到根的判别式为0,进而得到切点坐标,再根据两直线倾斜角之间的关系,得到b的值,从而得椭圆C的方程;(2)设出直线![]() 的方程,联立直线与椭圆方程,设出
的方程,联立直线与椭圆方程,设出![]() ,
,![]() ,可得
,可得![]() ,
,![]() 及
及![]() 坐标,写出直线
坐标,写出直线![]() 的方程,化简,根据方程的特点,即得
的方程,化简,根据方程的特点,即得![]() 过定点
过定点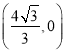 .
.
解:(1)由题意可知直线l的斜率存在且不为0,设直线l的方程为![]() ,与椭圆方程联立,得
,与椭圆方程联立,得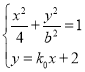 ,化简整理得
,化简整理得![]() ,(*)
,(*)
![]() ,得
,得![]() ,
,
所以方程(*)可化为![]() ,可得切点
,可得切点![]() .
.
![]() ,由已知
,由已知![]() ,
,
所以![]() ,即
,即![]() ,得
,得![]() ,
,
所以椭圆C的方程为![]() .
.
(2)由(1)知![]() ,
,
设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,得
,与椭圆方程联立,得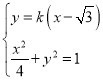 ,化简整理得
,化简整理得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
由![]() ,可得
,可得![]() ,则
,则
![]() 的方程为
的方程为![]() ,
,
即![]()
![]()
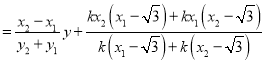
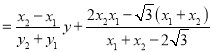
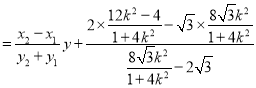
![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() 过定点
过定点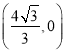 .
.
拓展结论:
圆![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在圆外,则直线方程
在圆外,则直线方程![]() 的几何含义是过点
的几何含义是过点![]() 所作圆的两条切线的切点连线的方程;由此类比:椭圆
所作圆的两条切线的切点连线的方程;由此类比:椭圆![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在椭圆外,则方程
在椭圆外,则方程![]() 的几何含义是过点
的几何含义是过点![]() 所作椭圆的两条切线的切点连线的方程;抛物线
所作椭圆的两条切线的切点连线的方程;抛物线![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在抛物线外,则直线方程
在抛物线外,则直线方程![]() 的几何含义是过点
的几何含义是过点![]() 所作抛物线的两条切线的切点连线的方程.
所作抛物线的两条切线的切点连线的方程.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 的准线方程为
的准线方程为![]() .
.
(1)求p的值;
(2)过抛物线C的焦点的直线l交抛物线C于点A,B,交抛物线C的准线于点P,若A为线段PB的中点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
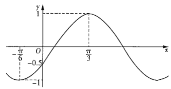
【题目】如图是函数![]() 的部分图象,把函数
的部分图象,把函数![]() 的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象向左平移
的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则下列说法正确的是( )
的图象,则下列说法正确的是( )
A.函数![]() 是偶函数
是偶函数
B.函数![]() 图象的对称轴为直线
图象的对称轴为直线![]()
C.函数![]() 的单调递增区间为
的单调递增区间为![]()
D.函数![]() 图象的对称中心为
图象的对称中心为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 的表达式和
的表达式和![]() 的递增区间;
的递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象.若函数
的图象.若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抖音是一款音乐创意短视频社交软件,是一个专注年轻人的15秒音乐短视频社区,用户可以通过这款软件选择歌曲,拍摄15秒的音乐短视频,形成自己的作品.2018年6月首批25家央企集体入驻抖音,一调研员在某单位进行刷抖音时间的调查,若该单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有3人是抖音迷,4人为非抖音迷,现从这7人中随机抽取3人做进一步的详细登记.
①用![]() 表示抽取的3人中是抖音迷的员工人数,求随机变量
表示抽取的3人中是抖音迷的员工人数,求随机变量![]() 的分布列与数学期望;
的分布列与数学期望;
②设![]() 为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件
为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com