
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,
,![]() 时,
时,![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,求出切点处的导数值,即为切线的斜率,求出
,求出切点处的导数值,即为切线的斜率,求出![]() ,由直线的点斜式方程可求出切线的方程.
,由直线的点斜式方程可求出切线的方程.
(2)分为![]() 和
和![]() 两种情况进行讨论,
两种情况进行讨论,![]() ,运用导数求出当
,运用导数求出当![]() ,
,![]() ,
,![]() 三种情况下的
三种情况下的![]() 的最值,从而可求出参数的取值范围.
的最值,从而可求出参数的取值范围.
(1)由![]() ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ,
,![]() , 当
, 当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() ,
,![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() .
.
令![]() ,则
,则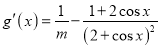 ,
,
设![]() ,则
,则![]() ,
,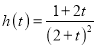 ,
,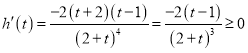 ,
,
所以![]() 在
在![]() 上递增,所以
上递增,所以![]() 的值域为
的值域为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 为
为![]() 上的增函数,
上的增函数,
所以![]() ,符合条件;
,符合条件;
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 为
为![]() 上的减函数,
上的减函数,
所以当![]() 时,
时,![]() ,不符合条件,舍去;
,不符合条件,舍去;
③当![]() ,即
,即![]() 时,存在
时,存在![]() ,使
,使![]() ,且
,且![]() 时,
时,![]() ,此时
,此时![]() ,不符合条件,舍去
,不符合条件,舍去
综上,所求的m的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某种新型病毒的传染能力很强,给人们生产和生活带来很大的影响,所以创新研发疫苗成了当务之急.为此,某药企加大了研发投入,市场上这种新型冠状病毒的疫苗![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 14 |
销量 | 1 | 1 | 2 | 2.5 | 4 | 4.5 |
(1)根据上表中的数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (用分数表示);
(用分数表示);
(2)根据所求的回归方程,估计当研发费用为1600万元时,销售量为多少?
参考公式: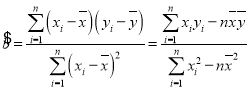 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,求圆
两点,求圆![]() 在
在![]() ,
,![]() 处两条切线的交点坐标.
处两条切线的交点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 与直线
与直线![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 做直线与曲线
做直线与曲线![]() 交于不同两点
交于不同两点![]() ,三角形
,三角形![]() 的垂心为点
的垂心为点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证:点![]() 在一条定直线上,并求出这条直线的方程.
在一条定直线上,并求出这条直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 的侧棱和底面垂直,且所有顶点都在球O的表面上,侧面
的侧棱和底面垂直,且所有顶点都在球O的表面上,侧面![]() 的面积为
的面积为![]() .给出下列四个结论:
.给出下列四个结论:
①若![]() 的中点为E,则
的中点为E,则![]() 平面
平面![]() ;
;
②若三棱柱![]() 的体积为
的体积为![]() ,则
,则![]() 到平面
到平面![]() 的距离为3;
的距离为3;
③若![]() ,
,![]() ,则球O的表面积为
,则球O的表面积为![]() ;
;
④若![]() ,则球O体积的最小值为
,则球O体积的最小值为![]() .
.
当则所有正确结论的序号是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点P的坐标是![]() ,曲线C的方程为
,曲线C的方程为![]() .以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为
.以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,斜率为![]() 的直线l经过点P.
的直线l经过点P.
(1)写出直线l的参数方程和曲线C的直角坐标方程;
(2)若直线l和曲线C相交于两点A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行排球比赛,采取五局三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩可知在每一局比赛中,甲队获胜的概率为![]() ,乙队获胜的概率为
,乙队获胜的概率为![]() .若前两局中乙队以
.若前两局中乙队以![]() 领先,则下列说法中错误的是( )
领先,则下列说法中错误的是( )
A.甲队获胜的概率为![]() B.乙队以
B.乙队以![]() 获胜的概率为
获胜的概率为![]()
C.乙队以三比一获胜的概率为![]() D.乙队以
D.乙队以![]() 获胜的概率为
获胜的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com