
【题目】已知函数![]() .
.
(Ⅰ)不需证明,直接写出![]() 的奇偶性:
的奇偶性:
(Ⅱ)讨论![]() 的单调性,并证明
的单调性,并证明![]() 有且仅有两个零点:
有且仅有两个零点:
(Ⅲ)设![]() 是
是![]() 的一个零点,证明曲线
的一个零点,证明曲线![]() 在点
在点![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线.
的切线.
【答案】(Ⅰ)奇函数;(Ⅱ)![]() 在
在![]() 和
和![]() 上单调递增;证明见解析;(Ⅲ)证明见解析.
上单调递增;证明见解析;(Ⅲ)证明见解析.
【解析】
(Ⅰ)先计算出函数的定义域,然后根据简单函数的奇偶性,简单判断可得结果.
(Ⅱ)计算函数![]() ,可得函数
,可得函数![]() 在
在![]() 和
和![]() 上单调递增,然后利用零点存在性定理以及函数的奇偶性,可得结果.
上单调递增,然后利用零点存在性定理以及函数的奇偶性,可得结果.
(Ⅲ)简单判断可知点![]() 在曲线
在曲线![]() 上,计算直线
上,计算直线![]() 的斜率以及曲线
的斜率以及曲线![]() 在点
在点![]() 处切线的斜率和曲线
处切线的斜率和曲线![]() 在点
在点![]() 处切线的斜率即可.
处切线的斜率即可.
(Ⅰ)定义域为![]() ,函数为奇函数.
,函数为奇函数.
(Ⅱ)因为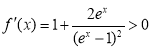 ,
,
由(Ⅰ)知,![]() 为奇函数,且
为奇函数,且![]()
所以,![]() 在
在![]() 和
和![]() 上单调递增.
上单调递增.
在![]() 上,
上,![]() ,
,
![]()
所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,即
,即![]() .
.
又![]() 为奇函数,
为奇函数,![]() .
.
故![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .
.
综上,![]() 有且仅有两个零点.
有且仅有两个零点.
(Ⅲ)因为![]() ,故点
,故点![]() 在曲线
在曲线![]() 上.
上.
由题设知![]() 即
即![]() ,连接
,连接![]() ,
,
则直线![]() 的斜率
的斜率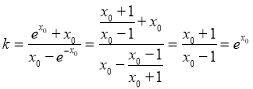
曲线![]() 在点
在点![]() 处切线的斜率是
处切线的斜率是![]() ;
;
曲线![]() 在点
在点![]() 处切线的斜率也是
处切线的斜率也是![]() .
.
所以曲线![]() 在点
在点![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线.
的切线.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】2019年女排世界杯(第13届女排世界杯)是由国际排联![]() 举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球
举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球![]() _
_![]() ,已知这种球的质量指标ξ(单位:
,已知这种球的质量指标ξ(单位:![]() )服从正态分布
)服从正态分布![]() .比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以
.比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分;而在比赛中以
取胜的球队积3分,负队积0分;而在比赛中以![]() 取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为
取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)如果比赛准备了1000个排球,估计质量指标在![]() 内的排球个数(计算结果取整数)
内的排球个数(计算结果取整数)
(2)第10轮比赛中,记中国队![]() 取胜的概率为
取胜的概率为![]() ,求出
,求出![]() 的最大值点
的最大值点![]() ,并以
,并以![]() 作为p的值,解决下列问题.
作为p的值,解决下列问题.
(i)在第10轮比赛中,中国队所得积分为X,求X的分布列;
(ii)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
参考数据:![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() 为两两不重合的平面,
为两两不重合的平面,![]() ,
,![]() ,
,![]() 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中真命题是( )
A.①③B.②④C.③④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的短轴的两个端点分别为
的短轴的两个端点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,且
的动点,且![]() 的面积最大值为
的面积最大值为![]() .
.
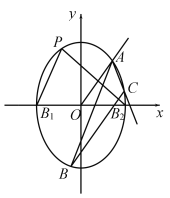
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点
作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点![]() 和点
和点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
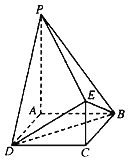
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是坐标原点,椭圆
是坐标原点,椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,若
在椭圆上,若![]() 的面积最大时
的面积最大时![]() 且最大面积为
且最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,点
,点![]() 是第四象限内的点且在椭圆
是第四象限内的点且在椭圆![]() 上,线段
上,线段![]() 被直线
被直线![]() 垂直平分,直线
垂直平分,直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com