
【题目】已知函数![]() .
.
(1)当函数![]() 与函数
与函数![]() 图象的公切线l经过坐标原点时,求实数a的取值集合;
图象的公切线l经过坐标原点时,求实数a的取值集合;
(2)证明:当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,且满足
,且满足![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先利用导数的几何意义和函数![]() 求出公切线方程,再将公切线方程与函数
求出公切线方程,再将公切线方程与函数![]() 联立,表示
联立,表示![]() ,再构造函数
,再构造函数![]() 利用导数求出其单调区间和值域,可求出a的取值;
利用导数求出其单调区间和值域,可求出a的取值;
(2)要证![]() 有两个零点,只要证
有两个零点,只要证![]() 有两个零点即可,而
有两个零点即可,而![]() 时函数
时函数![]() 的一个零点,所以只需再利用导数研究此函数的性质即可,由于两个零点,一个是
的一个零点,所以只需再利用导数研究此函数的性质即可,由于两个零点,一个是![]() ,另一个在区间
,另一个在区间![]() 上,若设
上,若设![]() 则
则![]() , 所以只需利用导数证明
, 所以只需利用导数证明![]() 即可 .
即可 .
解:(1)设公切线l与函数![]() 的切点为
的切点为![]() ,则公切线l的斜率
,则公切线l的斜率![]() ,公切线l的方程为:
,公切线l的方程为:![]() ,将原点坐标
,将原点坐标![]() 代入,得
代入,得![]() ,解得
,解得![]() ,公切线l的方程为:
,公切线l的方程为:![]() ,
,
将它与![]() 联立,整理得
联立,整理得![]() .
.
令![]() ,对之求导得:
,对之求导得:![]() ,令
,令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() 单调递减,值域为
单调递减,值域为![]() ,
,
当![]() 时,
时,![]() 单调递增,值域为
单调递增,值域为![]() ,
,
由于直线l与函数![]() 相切,即只有一个公共点,
相切,即只有一个公共点,
故实数a的取值集合为![]() .
.
(2)证明:![]() ,要证
,要证![]() 有两个零点,只要证
有两个零点,只要证![]() 有两个零点即可.
有两个零点即可.![]() ,即
,即![]() 时函数
时函数![]() 的一个零点.
的一个零点.
对![]() 求导得:
求导得:![]() ,令
,令![]() ,解得
,解得![]() .当
.当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减.当
单调递减.当![]() 时,
时,![]() 取最小值,
取最小值,![]() ,
,![]() ,必定存
,必定存![]() 在使得二次函数
在使得二次函数![]() ,
,
即![]() .因此在区间上
.因此在区间上![]() 必定存在
必定存在![]() 的一个零点.
的一个零点.
练上所述,![]() 有两个零点,一个是
有两个零点,一个是![]() ,另一个在区间
,另一个在区间![]() 上.
上.
下面证明![]() .
.
由上面步骤知![]() 有两个零点,一个是
有两个零点,一个是![]() ,另一个在区间
,另一个在区间![]() 上.
上.
不妨设![]() 则
则![]() ,下面证明
,下面证明![]() 即可.
即可.
令![]() ,对之求导得
,对之求导得![]() ,
,
故![]() 在定义域内单调递减,
在定义域内单调递减,![]() ,即
,即![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分别为线段
分别为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法正确的是( )
翻转过程中,下列说法正确的是( )
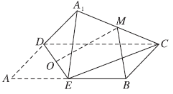
A.与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直
垂直
B.异面直线![]() 与
与![]() 所成的角是定值
所成的角是定值
C.一定存在某个位置,使![]()
D.三棱锥![]() 外接球半径与棱
外接球半径与棱![]() 的长之比为定值
的长之比为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域均为D的三个函数![]() ,
,![]() ,
,![]() 满足条件:对任意
满足条件:对任意![]() ,点
,点![]() 与点
与点![]() 都关于点
都关于点![]() 对称,则称
对称,则称![]() 是
是![]() 关于
关于![]() 的“对称函数”.已知函数
的“对称函数”.已知函数![]() ,
,![]() ,
,![]() 是
是![]() 关于
关于![]() 的“对称函数“,记
的“对称函数“,记![]() 的定义域为D,若对任意
的定义域为D,若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
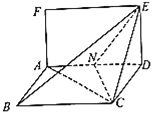
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“─”和“﹣﹣”,其中“─”在二进制中记作“1”,“﹣﹣”在二进制中记作“0”.如符号“”对应的二进制数011(2)化为十进制的计算如下:011(2)=0×22+1×21+1×20=3(10).若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受新冠肺炎疫情影响,某学校按上级文件指示,要求错峰放学,错峰有序吃饭.高三年级一层楼六个班排队,甲班必须排在前三位,且丙班、丁班必须排在一起,则这六个班排队吃饭的不同安排方案共有( )
A.240种B.120种C.188种D.156种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)不需证明,直接写出![]() 的奇偶性:
的奇偶性:
(Ⅱ)讨论![]() 的单调性,并证明
的单调性,并证明![]() 有且仅有两个零点:
有且仅有两个零点:
(Ⅲ)设![]() 是
是![]() 的一个零点,证明曲线
的一个零点,证明曲线![]() 在点
在点![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线.
的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com