
����Ŀ��2019��Ů�����籭����13��Ů�����籭�����ɹ�������![]() �ٰ�����£�������2019��9��14����9��29�����ձ����У�����12֧��������.���α����������µ���������
�ٰ�����£�������2019��9��14����9��29�����ձ����У�����12֧��������.���α����������µ���������![]() _
_![]() ����֪�����������ָ��Σ���λ��
����֪�����������ָ��Σ���λ��![]() ��������̬�ֲ�
��������̬�ֲ�![]() .�������Ʋ�ȡ��ѭ����ʽ����ÿ֧��ӽ���11�������������ѡ�����ھ�.���ֹ������£�������ȡ5��3ʤ�ƣ�����������
.�������Ʋ�ȡ��ѭ����ʽ����ÿ֧��ӽ���11�������������ѡ�����ھ�.���ֹ������£�������ȡ5��3ʤ�ƣ�����������![]() ��
��![]() ȡʤ����ӻ�3�֣����ӻ�0�֣����ڱ�������
ȡʤ����ӻ�3�֣����ӻ�0�֣����ڱ�������![]() ȡʤ����ӻ�2�֣����ӻ�1��.9�ֹ����ְ��ϵ�ǰ2���ֱ�Ϊ�й��Ӻ������ӣ��й��ӻ�26�֣������ӻ�22��.��10���й��ӶԿ�����ά�Ƕӣ���ÿ�ֱ����й���ȡʤ�ĸ���Ϊ
ȡʤ����ӻ�2�֣����ӻ�1��.9�ֹ����ְ��ϵ�ǰ2���ֱ�Ϊ�й��Ӻ������ӣ��й��ӻ�26�֣������ӻ�22��.��10���й��ӶԿ�����ά�Ƕӣ���ÿ�ֱ����й���ȡʤ�ĸ���Ϊ![]() .
.
��1�������������1000������������ָ����![]() �ڵ����������������ȡ������
�ڵ����������������ȡ������
��2����10�ֱ����У����й���![]() ȡʤ�ĸ���Ϊ
ȡʤ�ĸ���Ϊ![]() �����
�����![]() �����ֵ��
�����ֵ��![]() ������
������![]() ��Ϊp��ֵ�������������.
��Ϊp��ֵ�������������.
��i���ڵ�10�ֱ����У��й������û���ΪX����X�ķֲ��У�
��ii����֪��10�������ӻ�3�֣��ж��й����ܷ���ǰһ�ֶ�ùھ�����10�ֹ����������һ�ּ���11�ֽ����Σ��й��ӻ�����ࣩ�����ܣ������Ӧ�ĸ��ʣ������ܣ���˵������.
�ο����ݣ�![]() ����
����![]() ��
��
![]() ��
��![]() .
.
���𰸡���1��477������2��![]() ����i������������ii������ǰһ�ֶ�ùھ���
����i������������ii������ǰһ�ֶ�ùھ���![]() .
.
��������
��1������̬�ֲ�![]() ԭ��������������
ԭ��������������
��2�����ݶ���ֲ������![]() �������õ������
�������õ������![]() ȡ���ֵʱ
ȡ���ֵʱ![]() ��ֵ��
��ֵ��![]() ���ݱ������ֹ��ó��й��ӵ÷ֿ��ܵ�ȡֵ��Ȼ�������ֲ��У�
���ݱ������ֹ��ó��й��ӵ÷ֿ��ܵ�ȡֵ��Ȼ�������ֲ��У�![]() ��
��![]() �ķֲ��з������ɵó��ܷ���ǰһ�ֶ�ùھ�����������.
�ķֲ��з������ɵó��ܷ���ǰһ�ֶ�ùھ�����������.
�⣺��![]() ����
����![]()
��������ָ����![]() �ڵ��������ԼΪ
�ڵ��������ԼΪ![]() ��
��
��2��![]() ��
��![]() .
.
��![]() ����
����![]() .
.
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ����������
����������
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ��������.
��������.
����![]() �����ֵ��
�����ֵ��![]() .�Ӷ�
.�Ӷ�![]() .
.
![]()
![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() .
.
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 3 | 2 | 1 | 0 |
|
|
|
|
|
![]() ��
��![]() �����й���10�ֺ���ܻ���Ϊ29�֣������Ӽ����10�ֺ͵�11�ֶ���3�֣���11�ֹ�����ܻ�����28�֣�
�����й���10�ֺ���ܻ���Ϊ29�֣������Ӽ����10�ֺ͵�11�ֶ���3�֣���11�ֹ�����ܻ�����28�֣�![]() �����ԣ��й��������10�ֻ�3�֣������ǰһ�ֶ�ùھ��������Ϊ
�����ԣ��й��������10�ֻ�3�֣������ǰһ�ֶ�ùھ��������Ϊ![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �������
�������![]() Ϊ���Σ��ı���
Ϊ���Σ��ı���![]() Ϊƽ���ı��Σ�ƽ��
Ϊƽ���ı��Σ�ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е�.
���е�.
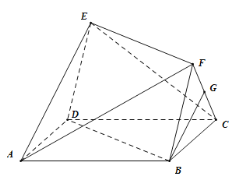
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Դ���ҹ��Ŵ��ġ�������������������������ķ��ţ������������������������������ڶ������м�����1�������������ڶ������м�����0���������������Ӧ�Ķ�������011��2����Ϊʮ���Ƶļ������£�011��2����0��22+1��21+1��20��3��10�������������������ȡ2�����Ž������У���õ��Ķ�����������Ӧ��ʮ����������2�ĸ���Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¹ڷ�������Ӱ�죬ijѧУ���ϼ��ļ�ָʾ��Ҫ������ѧ����������Է�.�����꼶һ��¥�������Ŷӣ��װ��������ǰ��λ���ұ��ࡢ�����������һ�������������ŶӳԷ��IJ�ͬ���ŷ������У� ��
A.240��B.120��C.188��D.156��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��е����ļ��νṹ���ü���������������ͬ��ֱ��������϶��ɵģ���ǰ�����ҡ����¾��Գƣ�ÿ���������ĵ��涼�DZ߳�Ϊ2�������Σ���Ϊ4���������������IJ��⻥�ഹֱ���������������________���棬�����Ϊ________��
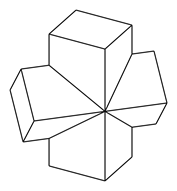
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ���ĵ�
���ĵ�![]() ��
��![]() ��
��![]() ��
��![]() ��ǡ������������Բ
��ǡ������������Բ![]() �ϣ����ҽ���ֱ�Ϊ
�ϣ����ҽ���ֱ�Ϊ![]() ��
��![]() ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() �Ҳ���������ƽ�е�ֱ��
�Ҳ���������ƽ�е�ֱ��![]() ����Բ��
����Բ��![]() ��
��![]() ���㣬���߶�
���㣬���߶�![]() �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽�![]() ���ڵ�
���ڵ�![]() ����
����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���Ʒ��۹������Ǻ��ȳ���������������Ӧ������٣�������˳�̨��ϵ�з��۵�������.ij���ⶨ��̨�����������������ߡ�.Ϊ�˽����Ƕԡ��������������ߡ���̬�ȣ���2060�����Ⱥ���������100�ˣ��������ݵ�Ƶ�ʷֲ�ֱ��ͼ��֧�֡����������������������ͳ�ƽ����ͼ��ʾ��
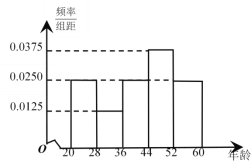
���� |
|
|
|
|
|
֧�ֵ����� | 15 | 5 | 15 | 28 | 17 |
��1��������ͳ��������![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��44��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��������������ߡ���֧�ֶ��в��죿
�����������ж��ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ��44��Ϊ�ֽ��IJ�ͬ��Ⱥ�ԡ��������������ߡ���֧�ֶ��в��죿
44������ | 44�꼰44������ | �ܼ� | |
֧�� | |||
��֧�� | |||
�ܼ� |
��2������44��Ϊ�ֽ�㣬�Ӳ�֧�֡��������������а��ֲ�����ķ�����ȡ8�˲μ�������֤�ᣬ�ִ���8���������2��.�dz鵽44�����ϵ�����Ϊ![]() �����������
�����������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�ο���ʽ��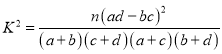 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
������֤����ֱ��д��![]() ����ż�ԣ�
����ż�ԣ�
��������![]() �ĵ����ԣ���֤��
�ĵ����ԣ���֤��![]() ���ҽ���������㣺
���ҽ���������㣺
������![]() ��
��![]() ��һ����㣬֤������
��һ����㣬֤������![]() �ڵ�
�ڵ�![]() ��������Ҳ������
��������Ҳ������![]() �����ߣ�
�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ���Ҷ�һ��������
���Ҷ�һ��������![]() ����
����![]() .
.
��1����֤��![]() ��
��
��2��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��3���Ƿ����ʵ��![]() ��ʹ����ʽ
��ʹ����ʽ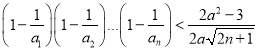 ����һ��������
����һ��������![]() �������������ڣ����
�������������ڣ����![]() ��ȡֵ��Χ���������ڣ���˵������.
��ȡֵ��Χ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com