
【题目】已知圆![]() 和定点
和定点![]() ,由圆
,由圆![]() 外一点
外一点![]() 向圆
向圆![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.

(1)求实数![]() 间满足的等量关系;
间满足的等量关系;
(2)若以![]() 为圆心的圆
为圆心的圆![]() 与圆
与圆![]() 有公共点,试求圆
有公共点,试求圆![]() 的半径最小时圆
的半径最小时圆![]() 的方程;
的方程;
(3)当![]() 点的位置发生变化时,直线
点的位置发生变化时,直线![]() 是否过定点,如果是,求出定点坐标,如果不是,说明理由.
是否过定点,如果是,求出定点坐标,如果不是,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)过定点
(3)过定点![]()
【解析】
试题分析:(1)由已知Q为切点,可知PQ⊥OQ,结合勾股定理有|PQ|2=|OP|2-|OQ|2及已知|PQ|=|PA|,利用两点间的距离公式可得a,b之间的关系;(2)设圆P的半径为R,由圆P与圆O有公共点,且半径最小,可知R=OP,利用两点间的距离,结合(1)中a,b的关系可转化为关于a的二次形式,结合二次函数的性质可求R的最小值,进而可求圆的方程;法二:圆P与圆O有公共点,圆P半径最小时为与圆O外切的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心为P过原点与l垂直的直线l'与l的交点P0,可求解;(3)首先由圆的方程求得直线![]() 方程,将其变形可求得所过定点
方程,将其变形可求得所过定点
试题解析:(1)连![]()
![]() 为切点,
为切点,![]() ,由勾股定理有
,由勾股定理有![]() .又由已知
.又由已知![]() ,故
,故![]() .
.
即:![]() .
.
化简得实数![]() 间满足的等量关系为:
间满足的等量关系为:![]() .
.
(2)解法1:设圆![]() 的半径为
的半径为![]() ,
,
![]() 圆
圆![]() 与圆
与圆![]() 有公共点,圆
有公共点,圆![]() 的半径为1,
的半径为1,
![]() 即
即![]() 且
且![]() .
.
而![]() ,故当
,故当![]() 时,
时,![]()
此时, ![]() ,
,![]() .得半径取最小值时圆
.得半径取最小值时圆![]() 的方程为
的方程为![]() .
.
解法2: 圆![]() 与圆
与圆![]() 有公共点,圆
有公共点,圆![]() 半径最小时为与圆
半径最小时为与圆![]() 外切(取小者)的情形,而这些半径的最小值为圆心
外切(取小者)的情形,而这些半径的最小值为圆心![]() 到直线
到直线![]() 的距离减去1,圆心
的距离减去1,圆心![]() 为过原点与
为过原点与![]() 垂直的直线
垂直的直线![]() 与
与![]() 的交点
的交点![]() .
.
![]() 又 直线
又 直线![]() 的方程为
的方程为![]()
解方程组![]() ,得
,得![]() .即
.即![]()
所以,所求圆方程为![]() .
.
(3)![]()
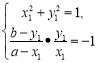 化简得
化简得![]() ,同理
,同理![]()
所以,直线MQ的方程为![]()
![]() ,代入上式得
,代入上式得
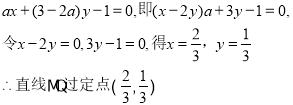


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,点D是AB的中点
=4,点D是AB的中点

(1)求证:AC![]() BC
BC![]() ;
;
(2)求证:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某公司技术升级后生产![]() 产品过程中记录的产量
产品过程中记录的产量![]() (吨)与相应的成本
(吨)与相应的成本![]() (万元)的几组对照数据:
(万元)的几组对照数据:

(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(3)已知该公司技术升级前生产100吨![]() 产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨
产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨![]() 产品的成本比技术升级前约降低多少万元?
产品的成本比技术升级前约降低多少万元?
(附:  ,
, ![]() ,其中
,其中![]() 为样本平均值)
为样本平均值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,二次函数
,二次函数![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,其中
,其中![]() 为非零常数,设
为非零常数,设![]() .
.
(1)求![]() 的值;
的值;
(2)若存在一条与![]() 轴垂直的直线和函数
轴垂直的直线和函数![]() 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当实数![]() 取何值时,函数
取何值时,函数![]() 存在极值?并求出相应的极值点.
存在极值?并求出相应的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与圆O:
与圆O:![]() 相交于A,B两个不同的点,且A
相交于A,B两个不同的点,且A![]() ,B
,B![]() .
.
(1)当![]() 面积最大时,求m的取值,并求出
面积最大时,求m的取值,并求出![]() 的长度.
的长度.
(2)判断![]() 是否为定值;若是,求出定值的大小;若不是,说明理由.
是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有8名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语,![]() 通晓俄语,
通晓俄语,![]() 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各![]() 名,组成一个小组.
名,组成一个小组.
(1)求![]() 被选中的概率;
被选中的概率;
(2)求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com