
【题目】设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 为偶函数时,求函数
为偶函数时,求函数![]() 的极值;
的极值;
(Ⅱ)若函数![]() 在区间
在区间![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)极小值![]() ,极大值
,极大值![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]()
【解析】
(Ⅰ)根据偶函数定义列方程,解得![]() .再求导数,根据导函数零点列表分析导函数符号变化规律,即得极值,(Ⅱ)先分离变量,转化研究函数
.再求导数,根据导函数零点列表分析导函数符号变化规律,即得极值,(Ⅱ)先分离变量,转化研究函数![]() ,
,![]() ,利用导数研究
,利用导数研究![]() 单调性与图象,最后根据图象确定满足条件的
单调性与图象,最后根据图象确定满足条件的![]() 的取值范围.
的取值范围.
(Ⅰ)由函数![]() 是偶函数,得
是偶函数,得![]() ,
,
即![]() 对于任意实数
对于任意实数![]() 都成立,
都成立,
所以![]() .
.
此时![]() ,则
,则![]() .
.
由![]() ,解得
,解得![]() .
.
当x变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() 有极小值
有极小值![]() ,
,![]() 有极大值
有极大值![]() .
.
(Ⅱ)由![]() ,得
,得![]() . 所以“
. 所以“![]() 在区间
在区间![]() 上有两个零点”等价于“直线
上有两个零点”等价于“直线![]() 与曲线
与曲线![]() ,
,![]() 有且只有两个公共点”.
有且只有两个公共点”.
对函数![]() 求导,得
求导,得![]() .
.
由![]() ,解得
,解得![]() ,
,![]() .
.
当x变化时,![]() 与
与![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
所以![]() 在
在![]() ,
,![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 或
或![]() 时,直线
时,直线![]() 与曲线
与曲线![]() ,
,![]() 有且只有两个公共点.
有且只有两个公共点.
即当![]() 或
或![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点.
上有两个零点.


科目:高中数学 来源: 题型:
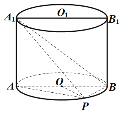
【题目】如图,已知点![]() 在圆柱
在圆柱![]() 的底面圆
的底面圆![]() 上,
上,![]() 为圆
为圆![]() 的直径.
的直径.
(1)若圆柱![]() 的体积
的体积![]() 为
为![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角(用反三角函数值表示结果);
所成的角(用反三角函数值表示结果);
(2)若圆柱![]() 的轴截面是边长为2的正方形,四面体
的轴截面是边长为2的正方形,四面体![]() 的外接球为球
的外接球为球![]() ,求
,求![]() 两点在球
两点在球![]() 上的球面距离.
上的球面距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年的政府工作报告强调,要树立绿水青山就是金山银山理念,以前所未有的决心和力度加强生态环境保护.某地科技园积极检查督导园区内企业的环保落实情况,并计划采取激励措施引导企业主动落实环保措施,下图给出的是甲、乙两企业2012年至2017年在环保方面投入金额(单位:万元)的柱状图.
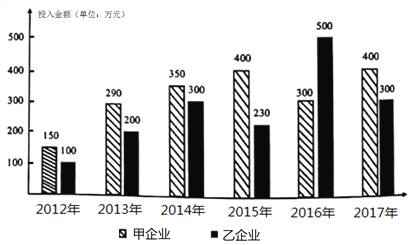
(Ⅰ)分别求出甲、乙两企业这六年在环保方面投入金额的平均数;(结果保留整数)
(Ⅱ)园区管委会为尽快落实环保措施,计划对企业进行一定的奖励,提出了如下方案:若企业一年的环保投入金额不超过200万元,则该年不奖励;若企业一年的环保投入金额超过200万元,不超过300万元,则该年奖励20万元;若企业一年的环保投入金额超过300万元,则该年奖励50万元.
(ⅰ)分别求出甲、乙两企业这六年获得的奖励之和;
(ⅱ)现从甲企业这六年中任取两年对其环保情况作进一步调查,求这两年获得的奖励之和不低于70万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(Ⅰ)当![]() ,且直线
,且直线![]()
![]() 轴时, 求四边形
轴时, 求四边形![]() 的面积;
的面积;
(Ⅱ)设![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:①“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若
互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若![]() ,则
,则![]() 有实数解”的逆否命题;④“若
有实数解”的逆否命题;④“若![]() ,则
,则![]() ”的逆否命题.其中真命题为________(填写所有真命题的序号).
”的逆否命题.其中真命题为________(填写所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com