
【题目】已知函数f(x)=2x-![]() ,x∈(0,1].
,x∈(0,1].
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在x∈(0,1]上是减函数,求实数a的取值范围.
【答案】(1)[2![]() ,+∞)(2)(-∞,-2]
,+∞)(2)(-∞,-2]
【解析】
(1)当a=-1时,f(x)=2x+![]() ,
,
因为0<x≤1,所以f(x)=2x+![]() ≥2
≥2![]() =2
=2![]() ,当且仅当x=
,当且仅当x=![]() 时,等号成立,
时,等号成立,
所以函数y=f(x)的值域是[2![]() ,+∞).
,+∞).
(2)(解法1)设0<x1<x2≤1,
由f(x1)-f(x2)=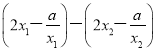 =2(x1-x2)+
=2(x1-x2)+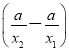 =
=![]() ,
,
因为函数y=f(x)在x∈(0,1]上是减函数,
所以f(x1)-f(x2)>0恒成立,
所以2x1x2+a<0,即a<-2x1x2在x∈(0,1]上恒成立,
所以a≤-2,即实数a的取值范围是(-∞,-2].
(解法2)由f(x)=2x-![]() ,知f′(x)=2+
,知f′(x)=2+![]() ,
,
因为函数y=f(x)在x∈(0,1]上是减函数,
所以f′(x)=2+![]() ≤0在x∈(0,1]上恒成立,
≤0在x∈(0,1]上恒成立,
即a≤-2x2在x∈(0,1]上恒成立,
所以a≤-2,即实数a的取值范围是(-∞,-2].


科目:高中数学 来源: 题型:
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况,调查部门在该校进行了一次问卷调查(共12道题),从该校学生中随机抽取40人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如下频率分布直方图.
六组,得到如下频率分布直方图.
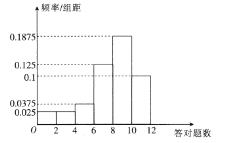
(1)若答对一题得10分,未答对不得分,估计这40人的成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ,顶点
,顶点![]() 在底面
在底面![]() 上的射影恰为点
上的射影恰为点![]() ,且
,且![]()

(1)证明:平面![]()
![]() 平面
平面![]() ;
;
(2)求棱![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(3)若点![]() 为
为![]() 的中点,并求出二面角
的中点,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,与
,与![]() 正半轴交于点
正半轴交于点![]() ,与直线
,与直线![]() 在第一象限的交点为
在第一象限的交点为![]() .点
.点![]() 为圆
为圆![]() 上任一点,且满足
上任一点,且满足![]() ,以
,以![]() 为坐标的动点
为坐标的动点![]() 的轨迹记为曲线
的轨迹记为曲线![]() .
.

(1)求圆![]() 的方程及曲线
的方程及曲线![]() 的方程;
的方程;
(2)若两条直线![]() 和
和![]() 分别交曲线
分别交曲线![]() 于点
于点![]() 和
和![]() ,求四边形
,求四边形![]() 面积的最大值,并求此时的
面积的最大值,并求此时的![]() 的值.
的值.
(3)根据曲线![]() 的方程,研究曲线
的方程,研究曲线![]() 的对称性,并证明曲线
的对称性,并证明曲线![]() 为椭圆.
为椭圆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的方程为![]() ,O为坐标原点,A为椭团的上顶点,
,O为坐标原点,A为椭团的上顶点,![]() 为其右焦点,D是线段
为其右焦点,D是线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆C的方程;
(2)过坐标原点且斜率为正数的直线交椭圆C于P,Q两点,分别作![]() 轴,
轴,![]() 轴,垂足分别为E,F,连接
轴,垂足分别为E,F,连接![]() ,
,![]() 并延长交椭圆C于点M,N两点.
并延长交椭圆C于点M,N两点.
(ⅰ)判断![]() 的形状;
的形状;
(ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
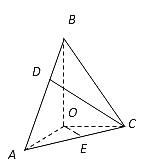
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,若存在,求出点
,若存在,求出点![]() 的
的
坐标;若不存在说明理由;
(3)若过![]() 点作直线
点作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,过
中,过![]() 轴正方向上一点
轴正方向上一点![]() 任作一直线,与抛物线
任作一直线,与抛物线![]() 相交于
相交于![]() 两点,一条垂直于
两点,一条垂直于![]() 轴的直线分别与线段
轴的直线分别与线段![]() 和直线
和直线![]() 交于点
交于点![]() .
.
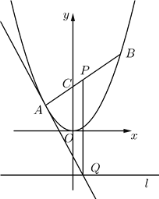
(1) 若![]() ,求
,求![]() 的值;
的值;
(2) 若![]() ,
,![]() 为线段
为线段![]() 的中点,求证: 直线
的中点,求证: 直线![]() 与该抛物线有且仅有一个公共点.
与该抛物线有且仅有一个公共点.
(3) 若![]() ,直线
,直线![]() 的斜率存在,且与该抛物线有且仅有一个公共点,试问
的斜率存在,且与该抛物线有且仅有一个公共点,试问![]() 是否一定为线段
是否一定为线段![]() 的中点? 说明理由.
的中点? 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列 ![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为数列
为数列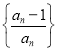 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com