
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的一个动点,当直线
轴上方的一个动点,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的另外一个交点为
的另外一个交点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意可得![]() ,
,![]() ,从而得到椭圆
,从而得到椭圆![]() 的方程;
的方程;
(2) 设直线![]() 的方程为
的方程为![]() 联立方程利用韦达定理表示面积,结合均值不等式即可得到最值.
联立方程利用韦达定理表示面积,结合均值不等式即可得到最值.
(1)方法一:∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
∴当直线![]() 的斜率为1时,直线
的斜率为1时,直线![]() 通过椭圆的上顶点,∴
通过椭圆的上顶点,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
方法二:设椭圆的右焦点为![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() . ①
. ①
又∵![]() ,∴
,∴![]() . ②
. ②
联立①②有![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
方法三:∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
∴椭圆![]() 的方程可化为
的方程可化为![]() ,即
,即![]() . ①
. ①
又直线![]() 的方程为
的方程为![]() . ②
. ②
联立①②有![]() ,即
,即![]() ,∴
,∴![]() 或
或![]() .
.
直线![]() 的斜率为1且
的斜率为1且![]() 在
在![]() 轴上方,∴
轴上方,∴![]() ,∴
,∴![]() 的坐标为
的坐标为![]() .
.
∴![]() ,又
,又![]() ,∴
,∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
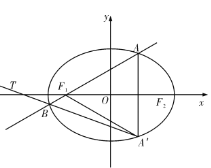
(2)∵![]() 在
在![]() 轴上方,∴直线
轴上方,∴直线![]() 的斜率不为0,设直线
的斜率不为0,设直线![]() 的方程为
的方程为![]() .
.
∵![]() ,
,![]() ,
,![]() 三点能构成三角形,∴直线
三点能构成三角形,∴直线![]() 不垂直于
不垂直于![]() 轴,∴
轴,∴![]() ,
,
设![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
联立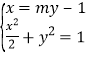 ,有
,有![]() ,即
,即![]() ,
,
∴![]() ,
,![]() .
.
方法一:![]()
![]()
![]() ,当且仅当
,当且仅当![]() 即
即![]() 时取等号.
时取等号.
∴![]() 面积的最大值为
面积的最大值为![]() .
.
方法二:直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则
![]()
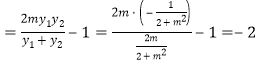 ,
,
∴直线![]() 过定点
过定点![]() ,设定点为
,设定点为![]() ,则
,则
![]()
![]()
![]() ,
,
当且仅当![]() 即
即![]() 时取等号.
时取等号.
∴![]() 面积的最大值为
面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年的政府工作报告强调,要树立绿水青山就是金山银山理念,以前所未有的决心和力度加强生态环境保护.某地科技园积极检查督导园区内企业的环保落实情况,并计划采取激励措施引导企业主动落实环保措施,下图给出的是甲、乙两企业2012年至2017年在环保方面投入金额(单位:万元)的柱状图.
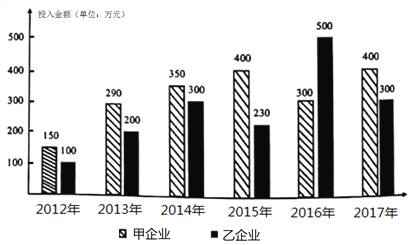
(Ⅰ)分别求出甲、乙两企业这六年在环保方面投入金额的平均数;(结果保留整数)
(Ⅱ)园区管委会为尽快落实环保措施,计划对企业进行一定的奖励,提出了如下方案:若企业一年的环保投入金额不超过200万元,则该年不奖励;若企业一年的环保投入金额超过200万元,不超过300万元,则该年奖励20万元;若企业一年的环保投入金额超过300万元,则该年奖励50万元.
(ⅰ)分别求出甲、乙两企业这六年获得的奖励之和;
(ⅱ)现从甲企业这六年中任取两年对其环保情况作进一步调查,求这两年获得的奖励之和不低于70万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:①“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若
互为倒数”的逆命题;②“面积相等的三角形全等”的否命题;③“若![]() ,则
,则![]() 有实数解”的逆否命题;④“若
有实数解”的逆否命题;④“若![]() ,则
,则![]() ”的逆否命题.其中真命题为________(填写所有真命题的序号).
”的逆否命题.其中真命题为________(填写所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 分别是
分别是![]() 的中点将
的中点将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 重合于点
重合于点![]() .则下列结论正确的是( )
.则下列结论正确的是( )

A. ![]()
B. 平面![]()
C. 二面角![]() 的余弦值为
的余弦值为![]()
D. 点![]() 在平面
在平面![]() 上的投影是
上的投影是![]() 的外心
的外心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com