Question

已知二次函数f（x）=x²+2bx+c（b，c∈R）．
（1）若f（x）≤0的解集为{x|-1≤x≤1}，求实数b，c的值；
（2）若f（x）满足f（1）=0，且关于x的方程f（x）+x+b=0的两个实根分别在区间（-3，-2）和（0，1）内，求实数b的取值范围．

Answer 1

分析：（1）利用不等式的解集的两端点值和对应方程根的关系求出b，c的值即可．
（2）先由f（1）=0得到关于b，c的关系式c=-2b-1，代入f（x）+x+b=0得g（x）=x²+（2b+1）x-b-1的图象与x轴的交点在区间（-3，-2）和（0，1）内，画出对应图象，借助于图象找到函数满足的条件，进而求出实数b的取值范围．

解答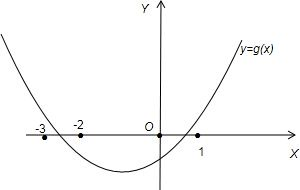：解：（1）因为f（x）≤0的解集为{x|-1≤x≤1}，
所以x²+2bx+c=0的根为-1，1．
故-1+1=-2b?b=0；
（-1）×1=c?c=-1．
所以b=0，c=-1．
（2）因为f（1）=0，所以1+2b+c=0?c=-2b-1．
所以f（x）+x+b=0即为x²+（2b+1）x-b-1=0．
令g（x）=x²+（2b+1）x-b-1
∵g（x）=f（x）+x+b=0的两个实根分别在区间（-3，-2）和（0，1）内，如图示
∴

g(0)＜0 g(1)＞0 g(-3)＞0 g(-2)＜0

?

b＞-1 b＞-1 b＞ 1 5 b＜ 5 7

?

1

5

＜b＜

5

7

故实数b的取值范围是

1

5

＜b＜

5

7

．

点评：本题考查一元二次方程根的分布与系数的关系．在解决这一类型题时，常常是把其对应函数找出来，借助于图象来解．函数的图象直观地显示了函数的性质．