
【题目】点![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为曲线
两点为曲线![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设出点![]() 的坐标,根据题意,列出方程,整理化简即可求得动点的轨迹方程;
的坐标,根据题意,列出方程,整理化简即可求得动点的轨迹方程;
(2)设出直线![]() 的方程,利用弦长公式求得
的方程,利用弦长公式求得![]() ,再利用
,再利用![]() ,建立直线
,建立直线![]() 与
与![]() 之间的联系,再利用点到直线的距离,以及面积公式,将四边形面积表示为函数形式,求该函数的值域即可.
之间的联系,再利用点到直线的距离,以及面积公式,将四边形面积表示为函数形式,求该函数的值域即可.
(1)设动点![]() ,则
,则![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由题可知:![]() ,即可得
,即可得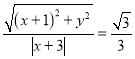 ,
,
两边平方整理可得:![]()
故曲线![]() 的方程为:
的方程为:![]() .
.
(2)因为![]() ,故
,故![]() 两点不可能重合,
两点不可能重合,
则直线![]() 的斜率不可能为0,
的斜率不可能为0,
故可设直线![]() 方程为
方程为![]() ,
,
联立椭圆方程![]() ,
,
可得![]() ,
,
设![]() 两点坐标分别为
两点坐标分别为![]() ,
,
则可得![]() ,
,
则![]()
故可得![]() ,
,
因为![]() ,故可得
,故可得![]() 四点共线,
四点共线,
故可得 .
.
不妨设直线![]() 方程为
方程为![]() ,
,![]() ,
,
联立直线![]() 与椭圆方程
与椭圆方程![]()
可得![]() ,
,
设![]() ,
,
则![]() ,即
,即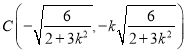
则![]() ,即
,即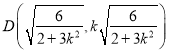
则点![]() 到直线
到直线![]() 的距离为:
的距离为:
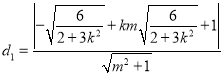
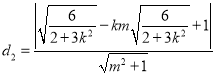
将![]() 代入上式即可得:
代入上式即可得:
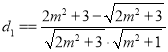 ,
,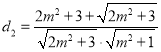 ,
,
故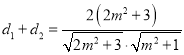
又根据弦长公式可得:
![]()
故四边形面积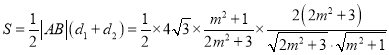
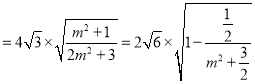 ,
,
因为![]() ,则
,则 ,
,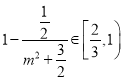 ,
,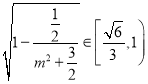
故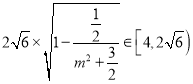 .
.
故四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,扇形AOB是一个观光区的平面示意图,其中圆心角∠AOB为![]() ,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
,半径OA为1 km.为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由弧AC、线段CD及线段DB组成,其中D在线段OB上,且CD∥AO.设∠AOC=θ.
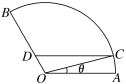
(1)用θ表示CD的长度,并写出θ的取值范围;
(2)当θ为何值时,观光道路最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】造纸术是我国古代四大发明之一.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中
系列,其中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格.
规格.![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() ,则这9张纸的面积之和等于______
,则这9张纸的面积之和等于______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com