练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】定义域均为D的三个函数，，满足条件：对任意，点与点都关于点对称，则称是关于的“对称函数”.已知函数，，是关于的“对称函数“，记的定义域为D，若对任意，都存在，使得成立，则实数a的取值范围是（ ）

    A..B..C..D..

    【答案】C

    【解析】

    求得的解析式和导数，以及单调性和极值、最值，进而得到的值域；判断在，递增，可得其值域，再由题意可得的值域包含在的值域内，可得的不等式组，解不等式可得所求范围．

    解：由函数，，是关于的“对称函数”，

    可得，，，，

    可得的解为，

    由，（1），，

    且在递增，，递减，可得的最小值为，最大值为1，

    可得的值域为，，

    而在，递增，可得的值域为，，

    由题意可得，，，

    即有，即为，

    解得或，

    则的范围是，

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四面体中，棱，所在直线所成角为，且，，，面和面所成的锐二面角为，面和面所成的锐二面角为，当四面体的体积取得最大值时（ ）.

    A.B.C.D.不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，不正确的是（ ）

    A.在中，若，则

    B.在锐角中，不等式恒成立

    C.在中，若，，则必是等边三角形

    D.在中，若，则必是等腰三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知分别为内角的对边，若是锐角三角形，需要同时满足下列四个条件中的三个：

    ① ② ③ ④

    （1）条件①④能否同时满足，请说明理由；

    （2）以上四个条件，请在满足三角形有解的所有组合中任选一组，并求出对应的的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是正方形，底面，，、分别是、上的点，且平面．

    （Ⅰ）求证：为的中点；

    （Ⅱ）当与平面所成的角最大时，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代十进制的算筹计数法，在数学史上是一个伟大的创造，算筹实际上是一根根同长短的小木棍．如图，是利用算筹表示数1－9的一种方法．例如：3可表示为“≡”，26可表示为“=⊥”，现有6根算筹，据此表示方法，若算筹不能剩余，则可以用1－9这9个数字表示两位数中，能被3整除的概率是（ ）

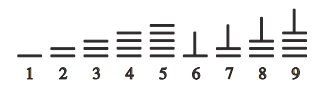
    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当函数与函数图象的公切线l经过坐标原点时，求实数a的取值集合；

    （2）证明：当时，函数有两个零点，且满足．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：x2＝2py（p＞0），F为抛物线C的焦点．以F为圆心，p为半径作圆，与抛物线C在第一象限交点的横坐标为2．

    （1）求抛物线C的方程；

    （2）直线y＝kx+1与抛物线C交于A，B两点，过A，B分别作抛物线C的切线l1，l2，设切线l1，l2的交点为P，求证：△PAB为直角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2016年春节期间全国流行在微信群里发抢红包，现假设某人将688元发成手气红包50个，产生的手气红包频数分布表如下：

    金额分组

    频 数

    3

    9

    17

    11

    8

    2

    （1）求产生的手气红包的金额不小于9元的频率；

    （2）估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表)；

    （3）在这50个红包组成的样本中，将频率视为概率．

    ①若红包金额在区间内为最佳运气手，求抢得红包的某人恰好是最佳运气手的概率；

    ②随机抽取手气红包金额在内的两名幸运者，设其手气金额分别为，，求事件“”的概率．

    查看答案和解析>>

    同步练习册答案