
����Ŀ��2019���ʮ����Ů�����籭��12֧������ӣ����������ȡ��ѭ����ʽ����ÿ֧��ӽ���11�������������ѡ�����ھ������ֹ������£�������ȡ5��3ʤ�ƣ�����������3��0��3��1ȡʤ����ӻ�3�֣����ӻ�0�֣����ڱ�������3��2ȡʤ����ӻ�2�֣����ӻ�1�֣�9�ֹ����ְ��ϵ�ǰ2���ֱ�Ϊ�й��Ӻ������ӣ��й��ӻ�26�֣������ӻ�22�֣���10���й��ӶԿ�����ά�Ƕӣ���ÿ�ֱ����й���ȡʤ�ĸ���Ϊ![]() ��
��
��1����10�ֱ����У����й���3��1ȡʤ�ĸ���Ϊ![]() ����
����![]() �����ֵ��
�����ֵ��![]() ��
��
��2���ԣ�1���е�![]() ��Ϊ
��Ϊ![]() ��ֵ��
��ֵ��
��i���ڵ�10�ֱ����У��й������û���Ϊ![]() ����
����![]() �ķֲ��У�
�ķֲ��У�
��������֪��10�������ӻ�3�֣��ж��й����ܷ���ǰһ�ֶ�ùھ�����10�ֹ����������һ�ּ���11�ֽ����Σ��й��ӻ�����ࣩ�����ܣ������Ӧ�ĸ��ʣ������ܣ���˵�����ɣ�
���𰸡���1����������2����i��������������������
��������
��1���ȵó�![]() ����ϵ����ó�����
����ϵ����ó�����![]() �ĵ����ԣ������ó�
�ĵ����ԣ������ó�![]() �����ֵ��
�����ֵ��![]() ��
��
��2����i���ȵó�![]() �Ŀ���ȡֵ���ٵó�����Ӧ���ʣ��г��ֲ��м��ɣ�
�Ŀ���ȡֵ���ٵó�����Ӧ���ʣ��г��ֲ��м��ɣ�
���������й����ڵ�10�ֱ����У����![]() ���֣����ܻ���Ϊ
���֣����ܻ���Ϊ![]() �֣����������ӵ�
�֣����������ӵ�![]() �����
�����![]() �֣����ܻ���Ϊ
�֣����ܻ���Ϊ![]() �֣����й��ӿ�����ǰһ�ֶ�ùھ�������ɣ�i���ó������.
�֣����й��ӿ�����ǰһ�ֶ�ùھ�������ɣ�i���ó������.
��1��![]()
�ɴ�![]()
��![]() ����
����![]()
��![]() ʱ��
ʱ��![]() ��
��![]() ����������
����������
��![]() ʱ��
ʱ��![]() ��
��![]() ����������
����������
����![]() �����ֵ��
�����ֵ��![]()
��2���ɣ�1��֪![]()
��i��![]() ��ȡ
��ȡ![]()
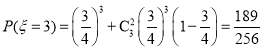


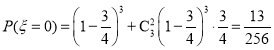
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
��������![]() �������
�����й���![]() �ֺ���ܻ���Ϊ
�ֺ���ܻ���Ϊ![]() �֣������Ӽ����
�֣������Ӽ����![]() �ֺ͵�
�ֺ͵�![]() �ֶ���
�ֶ���![]() �֣���
�֣���![]() �ֹ�����ܻ�����
�ֹ�����ܻ�����![]() �֣�
�֣�![]() �����ԣ��й��������
�����ԣ��й��������![]() �ֻ�
�ֻ�![]() �֣������ǰһ�ֶ�ùھ��������Ϊ
�֣������ǰһ�ֶ�ùھ��������Ϊ![]()


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1���жϺ���![]() �ڵ�
�ڵ�![]() ���������Ƿ�����㣿����������õ�����ꣻ����������˵�����ɣ�
���������Ƿ�����㣿����������õ�����ꣻ����������˵�����ɣ�
��2����![]() �����ֵ
�����ֵ![]() ��֤����
��֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������ҹ�������Ѹ�ͷ�չ��Ϊ���ǵij����ṩ�˱�������Ҳ�����еĽ�ͨ����������һЩ���ѣ�Ϊ���չ���������![]() ʡ�ķ�չ�����ij��������Ӹ�ʡ��ȡ��5�����У���ͳ���˹���������
ʡ�ķ�չ�����ij��������Ӹ�ʡ��ȡ��5�����У���ͳ���˹���������![]() ָ��
ָ��![]() ��
��![]() ָ��
ָ��![]() ���������±���ʾ��
���������±���ʾ��
����1 | ����2 | ����3 | ����4 | ����5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
��1������![]() ��
��![]() ������ϵ��
������ϵ��![]() ����˵��
����˵��![]() ��
��![]() �Ƿ���н�ǿ��������ع�ϵ����
�Ƿ���н�ǿ��������ع�ϵ����![]() ������Ϊ
������Ϊ![]() ��
��![]() ���н�ǿ��������ع�ϵ��������Ϊû�н�ǿ��������ع�ϵ��.
���н�ǿ��������ع�ϵ��������Ϊû�н�ǿ��������ع�ϵ��.
��2������![]() ����
����![]() �Ļع鷽�̣���Ԥ�
�Ļع鷽�̣���Ԥ�![]() ָ��Ϊ7ʱ��
ָ��Ϊ7ʱ��![]() ָ��Ĺ���ֵ.
ָ��Ĺ���ֵ.
��3����ij���еĹ�������![]() ָ��
ָ��![]() ������
������![]() ���Ҳ࣬����Ϊ�ó��й��������������࣬�Գ��еĽ�ͨ�����нϴ��Ӱ�콻ͨ�������Ž�����������ֱ��
���Ҳ࣬����Ϊ�ó��й��������������࣬�Գ��еĽ�ͨ�����нϴ��Ӱ�콻ͨ�������Ž�����������ֱ��![]() ָ��
ָ��![]() ������
������![]() ������֪
������֪![]() ʡij���й���������
ʡij���й���������![]() ָ��Ϊ13����ó��еĽ�ͨ���������Ƿ���Ҫ������������˵������.
ָ��Ϊ13����ó��еĽ�ͨ���������Ƿ���Ҫ������������˵������.
�ο���ʽ���ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
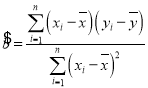 ����
����![]() ���ϵ��
���ϵ��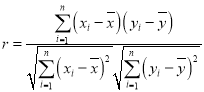
�ο����ݣ�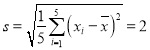 ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABC��A1B1C1�У�ƽ��ABC���µ��森M��BB1�ϵĵ㣬AB��3��BC��4��AC��5��CC1��7��������A��M��C1�����棬�������ܳ���Сʱ�����潫�������ֳɵ��ϡ��������ֵ������Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2020��2��15����3��2���人�������¹ڷ���ȷ�ﲡ��������ͳ��ͼ��������˵������ȷ���ǣ� ��

A.2020��2��19���人�������¹ڷ���ȷ�ﲡ������½�����λ��
B.�人�����¹ڷ������������ȡ���˽��Եijɹ���������Ҫ���ܽ���
C.2020��2��19����3��2���人�������¹ڷ���ȷ�ﲡ������400�˵���8��
D.2020��2��15�յ�3��2���人�������¹ڷ���ȷ�ﲡ������һ������ٵ�һ���1549��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ͳ�ƣ�2019���ȫ���ѿ�ͨ![]() ��վ13���������ʡ�е������������潫���ƽ�
��վ13���������ʡ�е������������潫���ƽ�![]() ͨ�����罨��������2020����ص㹤��������һ�·�ȫ��������վ3���.
ͨ�����罨��������2020����ص㹤��������һ�·�ȫ��������վ3���.
��1�������2�·����Ժ��ÿ���±���һ���¶ཨ��2000������ô�������ȫ�����л�վ�������.����ȷ��0.1�����
��2������ƻ������½���վ60�������2022���ȫ��������Ҫ800��������ң�����½�������ÿ�����һ���Եȱȵ�������2021���2022�����ٸ����������������ɼƻ�������ȷ��1�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĵ㣬
�ϵĵ㣬![]() ����
����![]() ����ͼ�٣�.���ı���
����ͼ�٣�.���ı���![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() ����ͼ�ڣ�.������Ĺ����У������б�����
����ͼ�ڣ�.������Ĺ����У������б�����

��![]() ƽ��
ƽ��![]() ��
��
���ĵ�![]() ��
��![]() ��
��![]() ��
��![]() ���ܹ��棻
���ܹ��棻
����![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ��
��
��ƽ��![]() ��ƽ��
��ƽ��![]() ���ܴ�ֱ.������ȷ����__________.
���ܴ�ֱ.������ȷ����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ1ֱ��������ACB�У�![]() ��
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ����
����![]() ��
��![]() ����ʹ��
����ʹ��![]() ��
��![]() ����ͼ2.
����ͼ2.
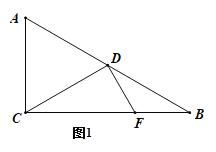
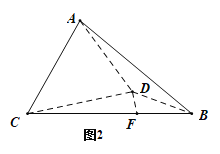
��1����֤��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊʵ������
Ϊʵ������![]() ����
����
����![]() ʱ��
ʱ��
����![]() ���жϺ���
���жϺ���![]() ����ż�ԣ���˵�����ɣ�
����ż�ԣ���˵�����ɣ�
����֤������![]() ��
��![]() ������������
������������
�����輯��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ����
��ȡֵ��Χ����![]() ��ʾ����
��ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com