
����Ŀ��ijѧУ�����꼶�ڿ�ѧʱ��������ѧ���.Ϊ���˽Ȿ�꼶ѧ�������ڼ���ʷ��ѧϰ������ִ��꼶![]() ���Ŀ����������ȡ��
���Ŀ����������ȡ��![]() ��ѧ�����ο��Ե���ʷ�ɼ����õ�������ʷ������Ƶ�ʷֲ�ֱ��ͼ��ͼ.��֪���ο��Ը����꼶��ʷ�ɼ��ֲ�����Ϊ
��ѧ�����ο��Ե���ʷ�ɼ����õ�������ʷ������Ƶ�ʷֲ�ֱ��ͼ��ͼ.��֪���ο��Ը����꼶��ʷ�ɼ��ֲ�����Ϊ![]() .
.

��1����ͼ��![]() ��ֵ��
��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������![]() ��ѧ����ʷ�ɼ���ƽ���֣���������ÿ�������ø���������е�ֵ��������
��ѧ����ʷ�ɼ���ƽ���֣���������ÿ�������ø���������е�ֵ��������
��3����֪��ѧУÿ��߿���![]() %��ͬѧ��ʷ�ɼ���һ�������ϣ���������������ķ�����������Ʊ�����ѧ�����ʷѧ�ƻ�����һ���߸�Ϊ���ٷ֣�
%��ͬѧ��ʷ�ɼ���һ�������ϣ���������������ķ�����������Ʊ�����ѧ�����ʷѧ�ƻ�����һ���߸�Ϊ���ٷ֣�
���𰸡���1��![]() ����2��ƽ����Ϊ
����2��ƽ����Ϊ![]() ������Ϊ
������Ϊ![]() ����3��
����3��![]() ��
��
��������
��1������Ƶ�ʺ�Ϊ![]() ���������
���������![]() ��ֵ��
��ֵ��
��2������Ƶ��ֱ��ͼ��ȡƵ����������ֵ��Ϊ��������ƽ������ʽ����������ۣ�
��3����ȷ����С������ʺ�Ϊ![]() ���ڵ��飬�Լ��ڸ������ڵı���������������.
���ڵ��飬�Լ��ڸ������ڵı���������������.
��1��������ã�![]() ��
��
���![]() ��
��
��2��������![]() ��ѧ����ʷ�ɼ���ƽ����Ϊ��
��ѧ����ʷ�ɼ���ƽ����Ϊ��
![]() ��
��
����Ϊ![]() ��
��
��3��![]() ��Ƶ�ʺ�Ϊ
��Ƶ�ʺ�Ϊ![]() ��
��![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]()
���Թ��Ʊ�����ѧ�����ʷѧ�ƻ�����һ����Ϊ![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������У�AD��ƽ��PDC���ı���ABCDΪƽ���ı��Σ���E��F�ֱ�ΪAD��BP���е㣬AD��3��AP��3![]() ��PC
��PC![]() ��
��
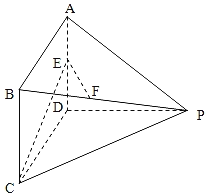
��1����֤��EF//ƽ��PDC��
��2������CDP��120����������E��CP��D��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ��֤����������
��֤����������![]() ������
������![]() ��ʹ��
��ʹ��![]() ��
��
��2����![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڶ����![]() �У��ı���
�У��ı���![]() Ϊ�������Σ�
��������![]() ��
��![]() ��
��![]() ���ı���
���ı���![]() Ϊֱ�����Σ�
Ϊֱ�����Σ�![]() ��
��![]() ����
����![]() Ϊ�ۺ۰ѵ�������
Ϊ�ۺ۰ѵ�������![]() ����ʹ��ƽ��
����ʹ��ƽ��![]() ƽ��
ƽ��![]() ����ͼ2��ʾ��
����ͼ2��ʾ��


��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������̵����߾������ɴ�ƽ�ƻ�ԳƱ任���ܹ���ȫ�غϣ��������������Ϊ����Ϊ���̶ԡ������������ĶԷ��̣�
��![]() ��
��![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]() ��
��![]()
������Ϊ���̶������ǣ� ��
A.�٢ڢ�B.�٢ۢ�C.�ڢۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() �������һ���˵㵽�ҽ���ľ���Ϊ2��
�������һ���˵㵽�ҽ���ľ���Ϊ2��

��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() �����Ҷ��㣬��ͼ������
�����Ҷ��㣬��ͼ������![]() �ֱ���ֱ��
�ֱ���ֱ��![]() ��
��![]() ����ֱ��
����ֱ��![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ����Բ
����Բ![]() ����һ��
����һ��![]() ���ֱ��
���ֱ��![]() ��
��![]() ����Բ
����Բ![]() ���������ߣ����������߽��ڵ�
���������ߣ����������߽��ڵ�![]() ���ֱ��
���ֱ��![]() ��
��![]() ����Բ
����Բ![]() ���������ߣ����������߽��ڵ�
���������ߣ����������߽��ڵ�![]() ��֤������
��֤������![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ������![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣬
���е㣬![]() ��
��![]() ��
Ϊ��![]() �ϵĵ㣮
�ϵĵ㣮
��1��֤����![]() ��
��
��2���Ƿ����һ��![]() ��ʹ��ƽ��
��ʹ��ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵΪ
���������ǵ�����ֵΪ![]() �������ڣ�˵����
�������ڣ�˵����![]() ��λ�ã��������ڣ�˵�����ɣ�
��λ�ã��������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ���Ҿ�����
���Ҿ����� ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������������ԭ���ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬������
���㣬������![]() ����
����![]() ������ʱֱ��
������ʱֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com