练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】用三种不同的颜色填涂如图3×3方格中的9个区域，要求每行、每列的三个区域都不同色，则不同的填涂方法种数共有（　　）

    A.48B.24C.12D.6

    【答案】B

    【解析】

    由题意知用三种不同颜色为9个区域涂色，第一步为第一行涂色，有A33种方法；第二步用与1号区域不同色的两种颜色为4、7两个区域涂色，有A22种方法；剩余区域只有一种涂法，根据分步计数原理得到结果．

    可将9个区域标号如图：

    用三种不同颜色为9个区域涂色，

    可分步解决：第一步，为第一行涂色，有A33＝6种方法；

    第二步，用与1号区域不同色的两种颜色为4、7两个区域涂色，有A22＝2种方法；

    剩余区域只有一种涂法，

    综上由分步乘法计数原理可知共有6×2＝12种涂法．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

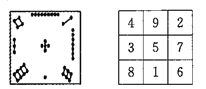
    【题目】我国古代的《洛书》中记载着世界上最古老的一个幻方：如图，将1，2，…，9填入的方格内，使三行，三列和两条对角线上的三个数字之和都等于15.一般地，将连续的正整数填入个方格中，使得每行，每列和两条对角线上的数字之和都相等，这个正方形叫做阶幻方.记阶幻方的对角线上的数字之和为，如图三阶幻方的，那么的值为__________ .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列是公差为2的等差数列，且成等比数列．数列满足：，.

    （Ⅰ）求数列，的通项公式；

    （Ⅱ）设数列的前n项和为，且，若对，恒成立，求正整数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司结合公司的实际情况针对调休安排展开问卷调查，提出了A，B，C三种放假方案，调查结果如下：

    （1）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持A方案”的人中抽取了6人，求n的值；

    （2）在“支持B方案”的人中，用分层抽样的方法抽取5人看作一个总体，从这5人中任意选取2人，求恰好有1人在35岁以上（含35岁）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B＝90°，AB＝BC＝2，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA1，E是A1C的中点．

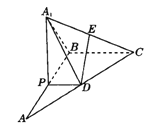
    （1）若P为AB的中点证明：DE∥平面PBA1．

    （2）若平面PDA1⊥平面PDA，且DE⊥平面CBA1，求二面角P﹣A1D﹣C的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛，从参加竞赛的学生中抽出60名学生，将其成绩（均为整数）分成六段，，…，后，画出如图所示的部分频率分布直方图.观察图形给出的信息，回答下列问题：

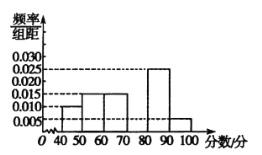
    （1）求第四组的频率，并补全这个频率分布直方图；

    （2）估计这次竞赛的及格率（60分及以上为及格）和平均分（同一组中的数据用该组区间的中点值代表）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn，等比数列{bn}的前n项和为Tn，a1=﹣1，b1=1，a2+b2=2．

    （1）若a3+b3=5，求{bn}的通项公式；

    （2）若T3=21，求S3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】朱世杰是元代著名数学家，他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作．《算学启蒙》中提到一些堆垛问题，如“三角垛果子”，就是将一样大小的果子堆垛成正三棱锥，每层皆堆成正三角形，从上向下数，每层果子数分别为1，3，6，10，…，现有一个“三角垛果子”，其最底层每边果子数为10，则该层果子数为（　　）

    A. 50B. 55C. 100D. 110

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公共汽车站有6个候车位排成一排，甲、乙、丙三个乘客在该汽车站等候228路公交车的到来，由于市内堵车，228路公交车一直没到站，三人决定在座位上候车，且每人只能坐一个位置，则恰好有2个连续空座位的候车方式的种数是( )

    A.48B.54C.72D.84

    查看答案和解析>>

    同步练习册答案