
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公切线的方程;
的公切线的方程;
(2)设函数![]() 的两个极值点为
的两个极值点为![]() ,求证:关于
,求证:关于![]() 的方程
的方程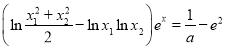 有唯一解.
有唯一解.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求两条曲线的公切线,分别求出各自的切线,然后两条切线为同一条直线,结合两个方程求解;
(2)要证明关于![]() 的方程
的方程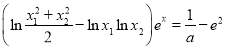 有唯一解,只要证明
有唯一解,只要证明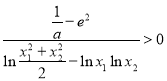 即可,由于当
即可,由于当![]() 时,
时,![]() 单调递增,不可能有两个零点,故
单调递增,不可能有两个零点,故![]() 不可能有两个极值点,故
不可能有两个极值点,故![]() ,利用
,利用![]() 得
得![]() ,又
,又![]()
![]() ,接下来只要证明
,接下来只要证明![]() ,即
,即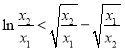 ,令
,令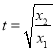 ,则只要证明
,则只要证明![]() 即可,用导数即可证明.
即可,用导数即可证明.
(1)曲线![]() 在切点
在切点![]() 处的切线方程为
处的切线方程为
![]() ,即
,即![]() ,
,
曲线![]() 在切点
在切点![]() 处的切线方程为
处的切线方程为
![]() ,即
,即![]() ,
,
由曲线![]() 与曲线
与曲线![]() 存在公切线,
存在公切线,
得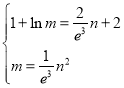 ,得
,得![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,∴
,∴![]() ,则
,则![]() ,
,
故公切线方程为![]() .
.
(2)要证明关于![]() 的方程
的方程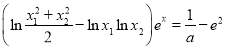 有唯一解,
有唯一解,
只要证明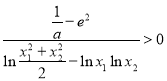 ,
,
先证明:![]() .
.
∵![]() 有两个极值点,
有两个极值点,
∴![]() 有两个不同的零点,
有两个不同的零点,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 单调递增,
单调递增,![]() 不可能有两个零点;
不可能有两个零点;
当![]() 时,
时,![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
又![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
∴![]() ,得
,得![]() ,∴
,∴![]() .
.
易知![]() ,
,
由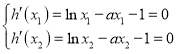 ,得
,得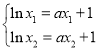 ,
,![]() ,
,
∴![]() .
.
下面再证明:![]() .
.
 ,
,
令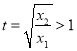 ,则只需证
,则只需证![]() ,
,
令![]() ,
,
则![]() ,
,
∴![]() ,得
,得![]() .
.
∴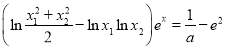 有唯一解.
有唯一解.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】某流行病爆发期间,某市卫生防疫部门给出的治疗方案中推荐了三种治疗药物![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
的使用是互斥且完备的),并且感染患者按规定都得到了药物治疗.患者在关于这三种药物的有关参数及市场调查数据如下表所示:(表中的数据都以一个疗程计)
|
|
|
|
单价(单位:元) | 600 | 1000 | 800 |
治愈率 |
|
|
|
市场使用量(单位:人) | 305 | 122 | 183 |
(Ⅰ)从感染患者中任取一人,试求其一个疗程被治愈的概率大约是多少?
(Ⅱ)试估算每名感染患者在一个疗程的药物治疗费用平均是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,右焦点到右准线的距离为3.
,右焦点到右准线的距离为3.
(1)求椭圆C的标准方程;
(2)过点P(0,1)的直线l与椭圆C交于两点A,B.己知在椭圆C上存在点Q,使得四边形OAQB是平行四边形,求Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面多边形![]() 中,
中,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
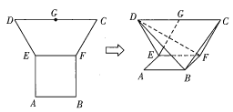
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为
的直线与抛物线交于A,B两点,又过A,B两点分作抛物线的切线,两条切线交于P点.记直线PA、PB的斜率分别为![]() 和
和![]() .
.
(1)求![]() 的值;
的值;
(2)![]() ,
,![]() ,求四边形PAEG面积的最小值.
,求四边形PAEG面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图平面PAC⊥平面ABC, AC⊥BC,PE// BC,M,N分别是AE,AP的中点,且△PAC是边长为2的等边三角形,BC=3,PE =2.

(1)求证:MN⊥平面PAC;
(2)求平面PAE与平面ABC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三年级学生在线学习情况,统计了2020年2月18日-27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.
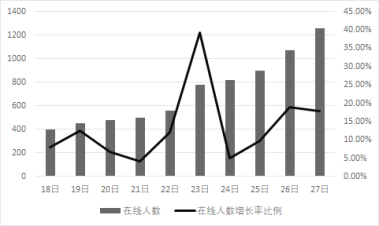
根据组合图判断,下列结论正确的是( )
A.前5天在线学习人数的方差大于后5天在线学习人数的方差
B.前5天在线学习人数的增长比例的极差大于后5天的在线学习人数的增长比例的极差
C.这10天学生在线学习人数的增长比例在逐日增大
D.这10天学生在线学习人数在逐日增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com