
已知椭圆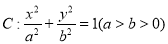 过点
过点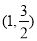 ,且离心率
,且离心率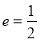 .
.
(1)求椭圆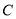 的标准方程;
的标准方程;
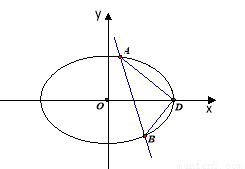
(2)若直线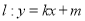 与椭圆
与椭圆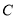 相交于
相交于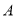 ,
,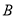 两点(
两点(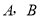 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为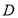 ,且满足
,且满足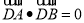 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
(1) 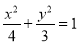 ;(2)
;(2)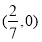 .
.
【解析】
试题分析:(1)本小题通过待定系数法列出两个关于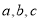 的方程,通过解方程组求出椭圆的方程,包含着二次方的运算需掌握;(2)本小题是直线与椭圆的位置关系的问题,这类题目的常用思路就是联立直线方程和椭圆方程通过消元得到一个一元二次方程,确定判别式的情况,正确书写、利用韦达定理,由
的方程,通过解方程组求出椭圆的方程,包含着二次方的运算需掌握;(2)本小题是直线与椭圆的位置关系的问题,这类题目的常用思路就是联立直线方程和椭圆方程通过消元得到一个一元二次方程,确定判别式的情况,正确书写、利用韦达定理,由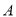 ,
,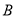 两点(
两点(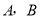 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为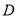 ,且满足
,且满足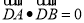 ,根据向量的数量积为零,可得到关于两个根的等式,再利用韦达定理可得关于
,根据向量的数量积为零,可得到关于两个根的等式,再利用韦达定理可得关于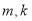 的等式,从而就可得出相应的结论.
的等式,从而就可得出相应的结论.
试题解析:(1)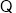
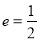
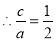 即
即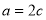
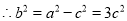
∴椭圆方程为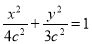 4分
4分
又点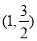 在椭圆上,
在椭圆上, 解得
解得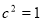
∴椭圆的方程为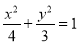 6分
6分
(2)设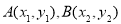 ,由
,由 得
得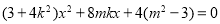
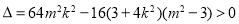 ,
,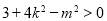
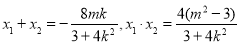 8分
8分
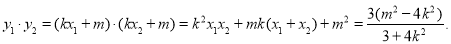
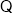
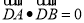
所以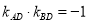 ,又椭圆的右顶点
,又椭圆的右顶点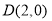
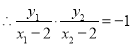 ,
,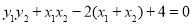
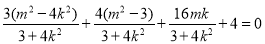
 ,解得 10分
,解得 10分
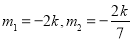 ,且满足
,且满足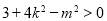
当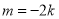 时,
时,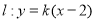 ,直线过定点
,直线过定点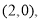 与已知矛盾 12分
与已知矛盾 12分
当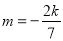 时,
时,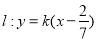 ,直线过定点
,直线过定点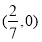
综上可知,当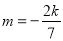 时,直线过定点,定点坐标为
时,直线过定点,定点坐标为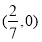 14分.
14分.
考点:1.直线与椭圆的位置关系;2.韦达定理;3.平面向量的数量积;4.过定点的问题;5.直线与椭圆的综合问题.


科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:选择题
已知p:函数f(x)=x2+mx+1有两个零点,q:?x∈R,4x2+4(m-2)x+1>0.若p∧?q为真,则实数m的取值范围为( ).
A.(2,3) B.(-∞,1]∪(2,+∞)
C.(-∞,-2)∪[3,+∞) D.(-∞,-2)∪(1,2]
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考文科数学试卷(解析版) 题型:选择题
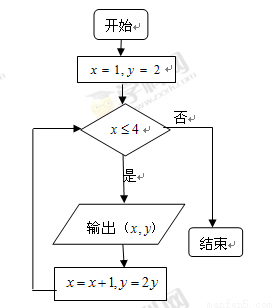
执行如右图所示的程序框图.则输出的所有点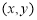 都在函数( )的图象上.
都在函数( )的图象上.
A. 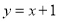 B.
B. 
C. 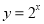 D.
D. 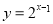
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
在棱长为1的正方体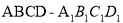 中,
中,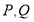 分别为线段
分别为线段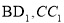 上的动点,则
上的动点,则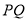 的最小值为( )
的最小值为( )
A. 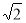 B.
B.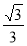 C.
C. 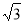 D.
D.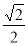
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
命题 方程
方程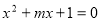 有实根,则
有实根,则 是( )
是( )
A.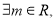 方程
方程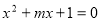 无实根
无实根
B. 方程
方程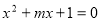 无实根
无实根
C.不存在实数 ,使方程
,使方程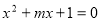 无实根
无实根
D.至多有一个实数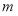 ,使方程
,使方程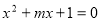 有实根
有实根
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末文科数学试卷(解析版) 题型:解答题
命题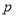 : 关于
: 关于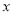 的不等式
的不等式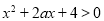 ,对一切
,对一切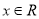 恒成立; 命题
恒成立; 命题 : 函数
: 函数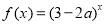 在
在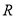 上是增函数.若
上是增函数.若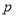 或
或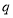 为真,
为真, 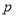 且
且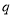 为假,求实数
为假,求实数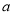 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末文科数学试卷(解析版) 题型:选择题
若 为两个定点且
为两个定点且 ,动点
,动点 满足
满足 ,则
,则 点的轨迹是( )
点的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com