练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某产品的广告费用x与销售额y的统计数据如下表

    广告费用x（万元）

    4

    2

    3

    5

    销售额y（万元）

    49

    26

    39

    54

    根据上表可得回归方程 = x+ 的 为9.4，据此模型预报广告费用为6万元时销售额为（ ）
    A.63.6万元
    B.65.5万元
    C.67.7万元
    D.72.0万元

    【答案】B
    【解析】解：∵ =3.5，
    =42，
    ∵数据的样本中心点在线性回归直线上，
    回归方程 = x+ 中的 为9.4，
    ∴42=9.4×3.5+a，
    ∴ =9.1，
    ∴线性回归方程是y=9.4x+9.1，
    ∴广告费用为6万元时销售额为9.4×6+9.1=65.5，
    故选：B．
    首先求出所给数据的平均数，得到样本中心点，根据线性回归直线过样本中心点，求出方程中的一个系数，得到线性回归方程，把自变量为6代入，预报出结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设m，n∈N，f（x）=（1+x）m+（1+x）n ．
    （1）当m=n=5时，若 ，求a0+a2+a4的值；
    （2）f（x）展开式中x的系数是9，当m，n变化时，求x2系数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，定义在[﹣1，2]上的函数f（x）的图象为折线段ACB，

    （1）求函数f（x）的解析式；
    （2）请用数形结合的方法求不等式f（x）≥log2（x+1）的解集，不需要证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在点处的切线方程为， （其中为常数）.

    （1）求函数的解析式；

    （2）若对任意，不等式恒成立，求实数的取值范围；

    （3）当时，求证： （其中e为自然对数的底数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某扇形的面积为4cm2 ， 周长为8cm，则此扇形圆心角的弧度数是；若点（a，9）在函数y=3x的图象上，则不等式 的解集为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在区间（﹣1，1）上的函数f（x）= 是奇函数，且f（ ）= ，
    （1）确定f（x）的解析式；
    （2）判断f（x）的单调性并用定义证明；
    （3）解不等式f（t﹣1）+f（t）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，，，是椭圆：（）的四个顶点，四边形是圆：的外切平行四边形，其面积为.椭圆的内接的重心（三条中线的交点）为坐标原点.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）的面积是否为定值？若是，求出该定值，若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知设函数f（x）=loga（1+2x）﹣loga（1﹣2x）（a＞0，a≠1）．
    （1）求f（x）的定义域；
    （2）判断f（x）的奇偶性并证明；
    （3）求使f（x）＞0的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本题满分12分）已知椭圆C： 的离心率为， 是椭圆的两个焦点， 是椭圆上任意一点，且的周长是．

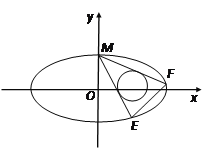
    （1）求椭圆C的方程；

    （2）设圆T： ，过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点，当圆心在轴上移动且时，求EF的斜率的取值范围．

    查看答案和解析>>

    同步练习册答案