
����Ŀ��������������ˮƽ�IJ�����ߣ�����������������.����������֯��WHO��������������ָ����BMI���������������ݳɶ��Լ��Ƿ�������㹫ʽ��![]() .���˵�BMI��ֵ��Ϊ��BMI
.���˵�BMI��ֵ��Ϊ��BMI![]() ƫ�ݣ�
ƫ�ݣ�![]() BMI
BMI![]() ������
������![]() BMI
BMI![]() Ϊƫ�֣�BMI
Ϊƫ�֣�BMI![]() Ϊ����.ij�о�����Ϊ�˽�ij��ݹ�˾Ա������������ָ�����о���Ա�ӹ�˾Ա����������У���ȡ��8��Ա�������1-8��������
Ϊ����.ij�о�����Ϊ�˽�ij��ݹ�˾Ա������������ָ�����о���Ա�ӹ�˾Ա����������У���ȡ��8��Ա�������1-8��������![]() ��cm��������
��cm��������![]() ��kg�����ݣ�������õ����ǵ�BMI����ȷ��0.1�����±���
��kg�����ݣ�������õ����ǵ�BMI����ȷ��0.1�����±���
�� �� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
���ߣ�cm�� | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
���أ�kg�� | 54 | 60 | 77 | 72 | 68 | �� | 72 | 55 |
BMI������ֵ�� | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
��1���ִ���8��Ա����ѡȡ3�˽��и��죬�dz�ȡ��BMIֵΪ��������Ա��������Ϊ![]() ����
����![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
��2���о������������ֹ�˾Ա��������![]() ��cm��������
��cm��������![]() ��kg��֮���н�ǿ��������ع�ϵ���ڱ��Ϊ6��������ݶ�ʧ֮ǰ����Ա���ѽ�����ص����ݷ�����������ó��������ݵ����Իع鷽��Ϊ
��kg��֮���н�ǿ��������ع�ϵ���ڱ��Ϊ6��������ݶ�ʧ֮ǰ����Ա���ѽ�����ص����ݷ�����������ó��������ݵ����Իع鷽��Ϊ![]() ���Ҹ��ݻع鷽��Ԥ��һ������Ϊ180cm��Ա������Ϊ71kg������õ��������������£�
���Ҹ��ݻع鷽��Ԥ��һ������Ϊ180cm��Ա������Ϊ71kg������õ��������������£�![]() ��
��![]() .
.
����![]() ��ֵ��������8��Ա�����ص�ƽ��ֵ
��ֵ��������8��Ա�����ص�ƽ��ֵ![]() .
.
�������ݴ���ʱ������Ա�ҷ��ֱ��Ϊ8��Ա��������������ӦΪ63kg��������������������ݵ���Ա�Ҹ������������¼������Իع鷽�̣����ݴ�Ԥ��һ������Ϊ180cm��Ա��������.
��������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ�� 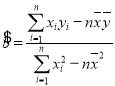 ��
��![]() .
.
���𰸡���1���ֲ��м�������![]() ����2����
����2����![]() ��
��![]() ����
����![]() ��75kg.
��75kg.
��������
��1�������![]() �Ŀ���ȡֵΪ0��1��2��3�������ùŵ���������Ӧ�ĸ��ʣ���д���ֲ��к������ý⣻
�Ŀ���ȡֵΪ0��1��2��3�������ùŵ���������Ӧ�ĸ��ʣ���д���ֲ��к������ý⣻
��2���������![]() �������������8��Ա�����ص�ƽ��ֵ
�������������8��Ա�����ص�ƽ��ֵ![]() �������
�������![]() ��
��![]() �����������������ݵ����Իع鷽��Ϊ
�����������������ݵ����Իع鷽��Ϊ![]() ����Ԥ��һ������Ϊ180cm��Ա��������.
����Ԥ��һ������Ϊ180cm��Ա��������.
�⣺��1��8��Ա��BMI��ֵΪ����������Ա����5�ˣ��dz鵽BMIֵΪ��������������Ϊ![]() ����
����![]() �Ŀ���ȡֵΪ0��1��2��3����
�Ŀ���ȡֵΪ0��1��2��3����
![]() ��
�� ![]() ��
��
![]() ��
�� ![]() .
.
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
| | | | |
��![]() .
.
��2���� ����Ա�������Իع鷽��![]() Ԥ��һ������Ϊ180cm��Ա��������Ϊ71kg���ɴ˼���
Ԥ��һ������Ϊ180cm��Ա��������Ϊ71kg���ɴ˼���![]() ����
����![]() .
.
�� �ɢ�֪����ǰ������![]() ��
��![]() .
.
��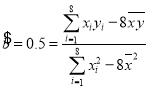 ��
��
![]() ��
��
�����������![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
����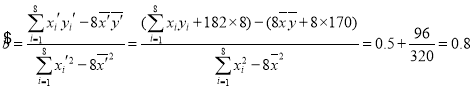 .
.
��![]() .
.
������������ݵ����Իع鷽��Ϊ![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
��������Ԥ��һ������Ϊ180cm��Ա��������Լ75kg.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y2=4x�Ľ����ֱ��l�������߽���A��B���㣬���M��3��0��.����MAB�����Ϊ![]() ����|AB|=( )
����|AB|=( )
A.2B.4C.![]() D.8
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���3��վ������6����̨���ϣ���ÿ��̨�����վ2�ˣ�ͬһ��̨���ϵ��˲�����վ��λ�ã���ͬ��վ�������ǣ� ��
A.90B.120C.210D.216
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̼�ͨ���������ֹ�ϵ������ȷ����Ʒ���ۼ۸�������Ʒ�����������a�����������b��b��a���Լ�����x��0��x��1��ȷ��ʵ�����ۼ۸�c=a+x��b��a�������x����Ϊ�ֹ�ϵ����
�������������ֹ�ϵ��xǡ��ʹ�ã�c��a���ǣ�b��c���ͣ�b��a���ĵȱ�����ݴ˿ɵã�����ֹ�ϵ��x��ֵ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʵ��![]() ���躯��
���躯��![]() .
.
��1����![]() ��
��![]() ʱ��֤����
ʱ��֤����![]() ��
��
��2����![]() ��������ֵ��
��������ֵ��![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �������Σ�
��������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ƽ��
ƽ��![]() ��
��
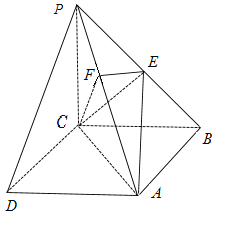
������֤��![]() Ϊ
Ϊ![]() ���е㣻
���е㣻
����![]() ��ƽ��
��ƽ��![]() ���ɵĽ����ʱ��������
���ɵĽ����ʱ��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ���϶���ΪM������M��б��Ϊ
���϶���ΪM������M��б��Ϊ![]() ��ֱ����
��ֱ����![]() ������һ��N����ԭ���ֱ��l��
������һ��N����ԭ���ֱ��l��![]() ����P��Q����
����P��Q����
��1����![]() �ܳ�����Сֵ��
�ܳ�����Сֵ��
��2���Ƿ����������ֱ�ߣ�ʹ����ֱ��![]() ƽ�е��ҵ��е㶼�ڸ�ֱ����?�����ڣ������ֱ�ߵķ��̣��������ڣ���˵������.
ƽ�е��ҵ��е㶼�ڸ�ֱ����?�����ڣ������ֱ�ߵķ��̣��������ڣ���˵������.
��3��ֱ��l���߶�![]() �ཻ�����ı���
�ཻ�����ı���![]() �����
�����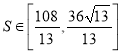 ����ֱ��l��б��k��ȡֵ��Χ.
����ֱ��l��б��k��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����������ߵ�����Ч�ʣ������������ߵ��豸�����˼�������.Ϊ�˶Աȼ���������Ч�����ɼ��������ߵļ�������ǰ���20�������������е�ʱ�䳤�ȣ���λ���죩���ݣ������������¾�Ҷͼ��
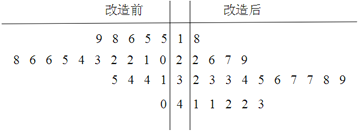
����1�������ɼ���40��������������ʱ�����λ��![]() ������������������ʱ�䳬��
������������������ʱ�䳬��![]() �Ͳ�����
�Ͳ�����![]() �Ĵ��������������������
�Ĵ��������������������
���� | ������ | |
����ǰ |
|
|
����� |
|
|
���![]() ��
��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2�����ݣ�1���е����������ܷ���![]() �İ�����Ϊ������������ǰ���������������ʱ���в��죿
�İ�����Ϊ������������ǰ���������������ʱ���в��죿
����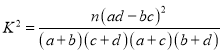 ��
��
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
�������������ߵ�������Ҫ����ά��.�����������ߵ�����ά�����ð�������ά���ѡ�����ά�������ֶ��������趨ά������Ϊ![]() �죨���ӿ������е���
�죨���ӿ������е���![]() �죨
�죨![]() ������ά��.��������һ���������������ü���ά�����ڣ�ÿ��ά�����������.��һ��ά�������ڣ������������������У����������ά���ѣ��������߲����������У����������ά����.�����㣬����ά����Ϊ0.5��Ԫ
������ά��.��������һ���������������ü���ά�����ڣ�ÿ��ά�����������.��һ��ά�������ڣ������������������У����������ά���ѣ��������߲����������У����������ά����.�����㣬����ά����Ϊ0.5��Ԫ![]() �Σ�����ά���ѵ�һ��Ϊ0.2��Ԫ
�Σ�����ά���ѵ�һ��Ϊ0.2��Ԫ![]() ���ڣ��˺�ÿ����һ������ά��������0.2��Ԫ.���ƶ�������һ���������ڣ���120��ƣ��ڵ�ά��������
���ڣ��˺�ÿ����һ������ά��������0.2��Ԫ.���ƶ�������һ���������ڣ���120��ƣ��ڵ�ά��������![]() ��
��![]() ��2��3��4.���������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ���һ����������������ά���ѵķֲ��м�����ֵ.
��2��3��4.���������ڼ��������һ��ά���������������������е�Ƶ����Ϊ���ʣ���һ����������������ά���ѵķֲ��м�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������C1�ļ����귽��Ϊ��sin����2��
��1��MΪ����C1�ϵĶ��㣬��P���߶�OM�ϣ�������![]() �����P�Ĺ켣C2��ֱ�����귽�̣�
�����P�Ĺ켣C2��ֱ�����귽�̣�
��2������C2������![]() ���B����2�����������OAB��������ֵ��
���B����2�����������OAB��������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com