
【题目】设数列![]() 的前
的前![]() 项和
项和![]() ,已知
,已知![]() ,
,![]() .
.
(1)求证:数列![]() 为等差数列,并求出其通项公式;
为等差数列,并求出其通项公式;
(2)设![]() ,又
,又![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 为正整数且
为正整数且![]() ,数列
,数列![]() 共有
共有![]() 项,设
项,设![]() ,又
,又![]() ,求
,求![]() 的所有可能取值.
的所有可能取值.
【答案】(1)证明见解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)当![]() 时,由所给的递推关系式进行作差变形证明后项与前项之差为常数即可证得数列为等差数列,进一步可得数列的通项公式;
时,由所给的递推关系式进行作差变形证明后项与前项之差为常数即可证得数列为等差数列,进一步可得数列的通项公式;
(2)结合(1)中的通项公式裂项求和,然后结合题意可确定实数![]() 的取值范围;
的取值范围;
(3)首先确定数列![]() 为等差数列,然后结合数列的单调性确定绝对值符号进行求和,得到关于k的不等式,最后求解关于k的不等式即可确定实数
为等差数列,然后结合数列的单调性确定绝对值符号进行求和,得到关于k的不等式,最后求解关于k的不等式即可确定实数![]() 的所有可能取值.
的所有可能取值.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
两式作差得![]() ,
,
故![]() ,
,
所以数列![]() 是公差为6的等差数列,
是公差为6的等差数列,
又![]() ,
,
所以![]() ;
;
(2)由于![]() ,故
,故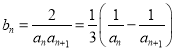 .
.
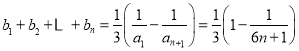 ,
,
显然![]() 单调递增,且
单调递增,且![]() ,
,
故![]() , 所以
, 所以![]() .
.
(3)![]() ,则
,则![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,
故当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
设数列![]() 的前n项和为
的前n项和为![]() ,于是:
,于是:
![]()
![]() ,
,
注意到![]() ,则
,则![]() ,题中的不等式即
,题中的不等式即![]() ,
,
所以![]() ,
,
所以,![]() 的所有可取值为
的所有可取值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: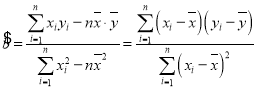 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.

(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )

A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:①对一切
满足:①对一切![]() 恒有
恒有![]() ;②对一切
;②对一切![]() 恒有
恒有![]() ;③当
;③当![]() 时,
时,![]() ,且
,且![]() ;④若对一切
;④若对一切![]() (其中
(其中![]() ),不等式
),不等式![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)证明:函数![]() 是
是![]() 上的递增函数;
上的递增函数;
(3)求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为矩形,且
为矩形,且![]() ,
,![]() ,若
,若![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.
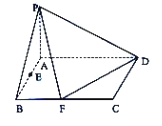
(1)证明:![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置:若不存在,说明理由;
的位置:若不存在,说明理由;
(3)若![]() 与平面
与平面![]() 所成的角为45°,求二面角
所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个孩子的身高![]() 与年龄
与年龄![]() (周岁)具有相关关系,根据所采集的数据得到线性回归方程
(周岁)具有相关关系,根据所采集的数据得到线性回归方程![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.回归直线一定经过样本点中心![]()
B.斜率的估计值等于6.217,说明年龄每增加一个单位,身高就约增加6.217个单位
C.年龄为10时,求得身高是![]() ,所以这名孩子的身高一定是
,所以这名孩子的身高一定是![]()
D.身高与年龄成正相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 的距离之和的最小值为__________.
的距离之和的最小值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com