
【题目】设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.
【答案】
(1)解:若f(0)≥1,则﹣a|a|≥1 ![]() a≤﹣1
a≤﹣1
(2)解:当x≥a时,f(x)=3x2﹣2ax+a2,∴ 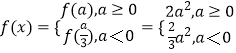 ,
,
如图所示:

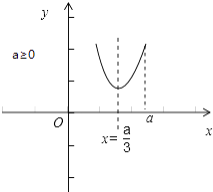
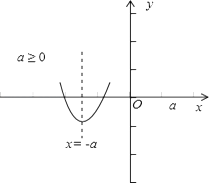
当x≤a时,f(x)=x2+2ax﹣a2,
∴ ![]() .
.

综上所述: 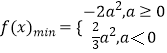 .
.
(3)解:x∈(a,+∞)时,h(x)≥1,
得3x2﹣2ax+a2﹣1≥0,△=4a2﹣12(a2﹣1)=12﹣8a2
当a≤﹣ ![]() 或a≥
或a≥ ![]() 时,△≤0,x∈(a,+∞);
时,△≤0,x∈(a,+∞);
当﹣ ![]() <a<
<a< ![]() 时,△>0,得:
时,△>0,得: 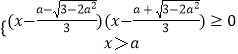
即 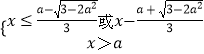
进而分2类讨论:
当﹣ ![]() <a<﹣
<a<﹣ ![]() 时,a<
时,a< ![]() ,
,
此时不等式组的解集为(a, ![]() ]∪[
]∪[ ![]() ,+∞);
,+∞);
当﹣ ![]() ≤x≤
≤x≤ ![]() 时,
时, ![]() <a<
<a< ![]() ;
;
此时不等式组的解集为[ ![]() ,+∞).
,+∞).
综上可得,
当a∈(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)时,不等式组的解集为(a,+∞);
,+∞)时,不等式组的解集为(a,+∞);
当a∈(﹣ ![]() ,﹣
,﹣ ![]() )时,不等式组的解集为(a,
)时,不等式组的解集为(a, ![]() ]∪[
]∪[ ![]() ,+∞);
,+∞);
当a∈[﹣ ![]() ,
, ![]() ]时,不等式组的解集为[
]时,不等式组的解集为[ ![]() ,+∞)
,+∞)
【解析】(1)f(0)≥1﹣a|a|≥1再去绝对值求a的取值范围,(2)分x≥a和x<a两种情况来讨论去绝对值,再对每一段分别求最小值,借助二次函数的对称轴及单调性.最后综合即可.(3)h(x)≥1转化为3x2﹣2ax+a2﹣1≥0,因为不等式的解集由对应方程的根决定,所以再对其对应的判别式分三种情况讨论求得对应解集即可.
【考点精析】掌握二次函数的性质和解一元二次不等式是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;求一元二次不等式
上递减;求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,AB=CD且异面直线AB与CD所成的角为30°,E,F为BC和AD的中点,则异面直线EF和AB所成的角为( )
A.15°
B.30°
C.45°或75°
D.15°或75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
x |
|
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式.
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为 ![]() ,当
,当 ![]() 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.![]()
B.![]()
C.[3,+∞)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x﹣6y+12=0,点A(3,5).
(1)求过点A的圆的切线方程;
(2)O点是坐标原点,连接OA,OC,求△AOC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.若 ![]() 与
与 ![]() 互为负向量,则
互为负向量,则 ![]() +
+ ![]() =0
=0
B.若 ![]()
![]() =0,则
=0,则 ![]() =
= ![]() 或
或 ![]() =
= ![]()
C.若 ![]() ,
, ![]() 都是单位向量,则
都是单位向量,则 ![]()
![]() =1
=1
D.若k为实数且k ![]() =
= ![]() ,则k=0或
,则k=0或 ![]() =
= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中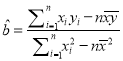 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com