
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,若直线
,若直线![]() 与函数
与函数![]() 的图象恰有11个不同的公共点,则实数
的图象恰有11个不同的公共点,则实数![]() 的取值范围为____________.
的取值范围为____________.
【答案】![]()
【解析】
根据对称性可知,![]() 时直线
时直线![]() 与函数
与函数![]() 的图象有6个交点,求得函数
的图象有6个交点,求得函数![]() 在
在![]() 上的解析式,并作出图象,可求得临界情况下
上的解析式,并作出图象,可求得临界情况下![]() 的值,进而可求得
的值,进而可求得![]() 的取值范围.
的取值范围.
由题意,函数![]() 和
和![]() 的图象都关于原点对称,则他们的图象交点也关于原点对称,
的图象都关于原点对称,则他们的图象交点也关于原点对称,
又![]() ,可知
,可知![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有6个交点.
的图象有6个交点.
当![]() 时,
时,![]() ,即
,即![]() ,则
,则![]() 时,
时,![]() ,
,
所以,![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
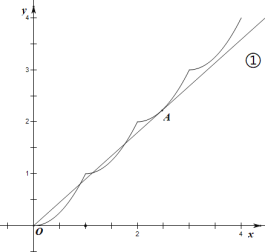
作出函数![]() 在
在![]() 上的图象,
上的图象,
①当直线![]() 与
与![]() 的图象在
的图象在![]() 处相切时,二者图象在
处相切时,二者图象在![]() 上5个交点,
上5个交点,
设切点为点![]() ,联立
,联立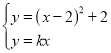 ,可得
,可得![]() ,则
,则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以只有
,所以只有![]() 符合题意;
符合题意;
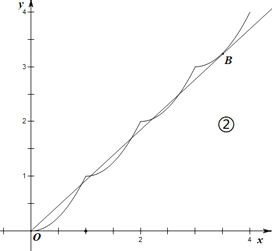
②当直线![]() 与
与![]() 的图象在
的图象在![]() 处相切时,二者图象在
处相切时,二者图象在![]() 上7个交点,
上7个交点,
设切点为点![]() ,联立
,联立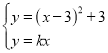 ,可得
,可得![]() ,则
,则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以只有
,所以只有![]() 符合题意;
符合题意;
显然,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 时有6个交点,根据对称性可知,此时直线
时有6个交点,根据对称性可知,此时直线![]() 与函数
与函数![]() 的图象恰有11个不同的公共点.
的图象恰有11个不同的公共点.
故答案为:![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自然状态下的鱼类是一种可再生资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用![]() 表示某鱼群在第
表示某鱼群在第![]() 年年初的总量且
年年初的总量且![]() .不考虑其他因素,设在第
.不考虑其他因素,设在第![]() 年内鱼群的繁殖量及捕捞量都与
年内鱼群的繁殖量及捕捞量都与![]() 成正比,死亡量与
成正比,死亡量与![]() 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数![]() ,
,![]() ,
,![]()
(1)求![]() 与
与![]() 的关系式
的关系式
(2)若每年年初鱼群的总量保持不变,求![]() ,
,![]() ,
,![]() ,
,![]() 所应满足的条件
所应满足的条件
(3)设![]() ,
,![]() ,为保证对任意
,为保证对任意![]() ,都有
,都有![]() ,则捕捞强度
,则捕捞强度![]() 的最大允许值是多少?并说明理由.
的最大允许值是多少?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲乙两地相距100海里,船从甲地匀速驶到乙地,已知某船的最大船速是36海里/时:当船速不大于每小时30海里/时,船每小时使用的燃料费用和船速成正比;当船速不小于每小时30海里/时,船每小时使用的燃料费用和船速的平方成正比;当船速为30海里/时,它每小时使用的燃料费用为300元;其余费用(不论船速为多少)都是每小时480元;
(1)试把每小时使用的燃料费用P(元)表示成船速v(海里/时)的函数;
(2)试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数;
(3)当船速为每小时多少海里时,船从甲地到乙地所需要的总费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若存在常数
,若存在常数![]() ,对任意
,对任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为T倍周期函数.
为T倍周期函数.
(1)判断![]() 是否是T倍周期函数,并说明理由;
是否是T倍周期函数,并说明理由;
(2)证明 是T倍周期函数,且T的值是唯一的;
是T倍周期函数,且T的值是唯一的;
(3)若![]() 是2倍周期函数,
是2倍周期函数,![]() ,
,![]() ,
,![]() 表示
表示![]() 的前n项和,
的前n项和,![]() ,若
,若![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设动直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
证明:以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() )
)
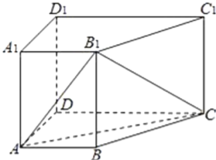
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值;
的值;
(3)现将与四棱柱![]() 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为![]() ,写出
,写出![]() 的解析式.(直接写出答案,不必说明理由)
的解析式.(直接写出答案,不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com