
【题目】已知函数![]() ,若存在常数
,若存在常数![]() ,对任意
,对任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为T倍周期函数.
为T倍周期函数.
(1)判断![]() 是否是T倍周期函数,并说明理由;
是否是T倍周期函数,并说明理由;
(2)证明 是T倍周期函数,且T的值是唯一的;
是T倍周期函数,且T的值是唯一的;
(3)若![]() 是2倍周期函数,
是2倍周期函数,![]() ,
,![]() ,
,![]() 表示
表示![]() 的前n项和,
的前n项和,![]() ,若
,若![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)不是,理由见解析;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)假设![]() 是T倍周期函数,推出矛盾即可说明
是T倍周期函数,推出矛盾即可说明![]() 不是T倍周期函数;
不是T倍周期函数;
(2)根据定义,可得到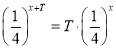 对任意x恒成立,即可求出
对任意x恒成立,即可求出![]() 的值,证明唯一性即可;
的值,证明唯一性即可;
(3)由![]() 是2倍周期函数,可求出
是2倍周期函数,可求出![]() 的奇数项和偶数项,进而可求得
的奇数项和偶数项,进而可求得![]() 和
和![]() ,从而求得
,从而求得![]() 的表达式,然后判断数列
的表达式,然后判断数列![]() 的单调性,可求得
的单调性,可求得![]() ,使得
,使得![]() ,解不等式即可.
,解不等式即可.
(1)不是,
假设![]() 是T倍周期函数,则
是T倍周期函数,则![]() ,
,
则![]() 对任意x恒成立,
对任意x恒成立,
显然![]() 不存在,所以
不存在,所以![]() 不是T倍周期函数.
不是T倍周期函数.
(2)设![]() ,
,
则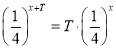 对任意x恒成立,
对任意x恒成立,
即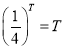 ,则
,则![]() ,
,
下证唯一性:
若![]() ,
,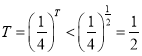 矛盾,
矛盾,
若![]() ,
,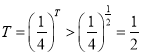 矛盾
矛盾
![]()
![]() 是唯一的;
是唯一的;
(3)![]() ,
,
![]() ,
,
![]() ,
,
…
![]() ,
,
所以![]() ,
,
同理:![]() ,
,
![]()
![]() ,
,
![]() .
.
则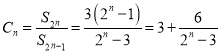 ,
,![]() ,
,![]() ,
,
显然![]() 时,
时,![]() ,
,
因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 时,数列
时,数列![]() 是递减数列,
是递减数列,
![]()
![]() ,
,
![]()
![]() 恒成,
恒成,
![]()
![]() ,
,
![]()
![]() ,
,
若![]() 时,则
时,则![]() ,解得
,解得![]() ;
;
若![]() 时,
时,![]() ,解得
,解得![]() ,
,
综上,a的取值范围是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)定义![]() ,证明:若存在
,证明:若存在![]() ,使得
,使得![]() 、
、![]() 为整数,且
为整数,且![]() 有两个整数零点,则必有无穷多个
有两个整数零点,则必有无穷多个![]() 有两个整数零点.
有两个整数零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左右两个焦点,过
的左右两个焦点,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),
在第一象限),![]() 的周长为8,
的周长为8,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为
为![]() 的左右顶点,直线
的左右顶点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,规定90分及以上为合格:
,规定90分及以上为合格:
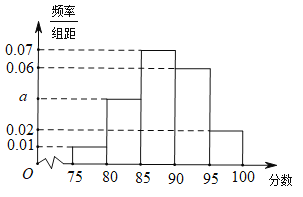
(1)求图中a的值;
(2)根据频率分布直方图估计该地区学员交通法规考试合格的概率;
(3)若三个人参加交通法规考试,估计这三个人至少有两人合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】日照一中为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
(1)试用x表示S,并求S的取值范围;
(2)若在矩形AMPN以外(阴影部分)铺上草坪.已知:矩形AMPN健身场地每平方米的造价为![]() ,草坪的每平方米的造价为
,草坪的每平方米的造价为![]() (k为正常数).设总造价T关于S的函数为T=f(S),试问:如何选取|AM|的长,才能使总造价T最低.
(k为正常数).设总造价T关于S的函数为T=f(S),试问:如何选取|AM|的长,才能使总造价T最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() 都有
都有![]() 成立,试求
成立,试求![]() 的取值范围;
的取值范围;
(3)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com