
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线MP与直线NP的斜率之积为
满足直线MP与直线NP的斜率之积为![]() .记动点P的轨迹为曲线C.
.记动点P的轨迹为曲线C.
(1)求曲线C的方程,并说明C是什么曲线;
(2)过点![]() 作直线
作直线![]() 与曲线C交于不同的两点A,B,试问在x轴上是否存在定点Q,使得直线QA与直线QB恰好关于x轴对称?若存在,求出点Q的坐标;若不存在,请说明理由.
与曲线C交于不同的两点A,B,试问在x轴上是否存在定点Q,使得直线QA与直线QB恰好关于x轴对称?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]()
![]() ,C为中心在坐标原点,焦点在
,C为中心在坐标原点,焦点在![]() 轴上的椭圆,不含左右顶点;(2)存在,
轴上的椭圆,不含左右顶点;(2)存在,
【解析】
(1)写出斜率,根据斜率之积为![]() 建立方程,化简即可;
建立方程,化简即可;
(2)设直线![]() 的方程为
的方程为![]() ,与椭圆C的方程联立整理得
,与椭圆C的方程联立整理得![]() ,设
,设![]() ,
,![]() ,定点
,定点![]() (依题意
(依题意![]() ).由根与系数的关系可得,
).由根与系数的关系可得,![]() ,
,![]() ,由直线
,由直线![]() 与直线
与直线![]() 恰好关于x轴对称,则直线
恰好关于x轴对称,则直线![]() 与直线
与直线![]() 的斜率互为相反数,代入可得.
的斜率互为相反数,代入可得.
(1)由题设可得![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() ,化简得.
,化简得. ![]()
![]() ,
,
所以C为中心在坐标原点,焦点在X轴上的椭圆,不含左右顶点.
(2)存在定点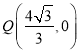 ,满足直线QA与直线QB恰好关于x轴对称,
,满足直线QA与直线QB恰好关于x轴对称,
由题设知,直线l的斜率不为0,设直线![]() 的方程为
的方程为![]() ,
,
与椭圆C的方程联立整理得![]() ,设
,设![]() ,
,![]() ,定点
,定点![]() (依题意
(依题意![]() ).
).
由根与系数的关系可得,![]() ,
,![]()
直线![]() 与直线
与直线![]() 恰好关于x轴对称,则直线
恰好关于x轴对称,则直线![]() 与直线
与直线![]() 的斜率互为相反数,
的斜率互为相反数,
所以![]() ,即
,即![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 整理得
整理得![]() .
.
从而可得![]() 即,
即,![]()
所以当![]() ,即
,即![]() 时,直线
时,直线![]() 与直线
与直线![]() 恰好关于x轴对称
恰好关于x轴对称
所以,在![]() 轴上存在点,
轴上存在点,![]() 满足直线
满足直线![]() 与直线
与直线![]() 恰好关于x轴对称
恰好关于x轴对称


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农业银行广元分行发行“金穗广元·剑门关旅游卡”是以“游广元、知广元、爱广元、共享和谐广元”为主题活动的一项经济性和公益性相结合的重大举措,以最优惠的价格惠及广元户籍市民、浙江及黑龙江援建省群众、省内援建市市民,凡上述对象均可办理此卡,本人凭此卡及本人身份证一年内(期满后可重新充值办理)在广元市范围内可无限次游览所有售门票景区景点,如:剑门关、朝天明月峡、旺苍鼓城山—七里峡、青川唐家河、广元皇泽寺、苍溪梨博园、昭化古城等,现有浙江及黑龙江援建省群众甲乙两人准备到广元旅游(同游),他们决定游览上面![]() 个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
个景点,首先游览剑门关但不能最后游览朝天明月峡的游览顺序有( )种.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抗击新冠肺炎的疫情中,某医院从3位女医生,5位男医生中选出4人参加援鄂医疗队,至少有一位女医生入选,其中女医生甲和男医生乙不能同时参加,则不同的选法共有种______(用数字填写答案).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 经过点
经过点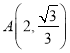 ,两个焦点为
,两个焦点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上一点,直线
上一点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,证明:当
,证明:当![]() 点在
点在![]() 上移动时,
上移动时,![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com