
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点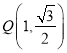 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)证明见解析;(ii)
;(Ⅱ)(i)证明见解析;(ii)![]() .
.
【解析】
(Ⅰ)根据题意可知,![]() ,
,![]() ,再结合
,再结合![]() 即可解出
即可解出![]() ,得到
,得到
椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)(i)根据直线![]() ,
,![]() 的斜率都存在或者直线
的斜率都存在或者直线![]() ,
,![]() 其中一条直线斜率不存在分类讨论,当直线
其中一条直线斜率不存在分类讨论,当直线![]() ,
,![]() 的斜率都存在时,联立直线与椭圆方程,根据
的斜率都存在时,联立直线与椭圆方程,根据![]() 可得直线
可得直线![]() ,
,![]() 的斜率的关系,结合点
的斜率的关系,结合点![]() 在圆
在圆![]() 上可得
上可得![]() ,即证出
,即证出![]() ,当直线
,当直线![]() 或
或![]() 的斜率不存在时,可确定点
的斜率不存在时,可确定点![]() 坐标,即可求出
坐标,即可求出![]() ,
,![]() 两点坐标,易得
两点坐标,易得![]() ;
;
(ii)设出点![]() ,
,![]() ,分类讨论直线
,分类讨论直线![]() 的斜率存在时以及不存在时的情况,由直线
的斜率存在时以及不存在时的情况,由直线![]() 的方程与椭圆方程联立可得
的方程与椭圆方程联立可得![]() ,即可得到直线
,即可得到直线![]() 的斜率存在或不存在时的方程为
的斜率存在或不存在时的方程为![]() ,同理可得直线
,同理可得直线![]() 的方程为
的方程为![]() ,即可得直线
,即可得直线![]() 的方程为
的方程为![]() ,再与椭圆方程联立求得弦长
,再与椭圆方程联立求得弦长![]() ,由点到直线的距离公式求出点
,由点到直线的距离公式求出点![]() 到直线
到直线![]() 的距离,从而得到
的距离,从而得到![]() 的面积的表达式,再根据换元法以及函数值域的求法即可求解.
的面积的表达式,再根据换元法以及函数值域的求法即可求解.
(Ⅰ)∵椭圆![]() 的左焦点
的左焦点![]() ,∴
,∴![]() .
.
将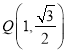 代入
代入![]() ,得
,得![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)设点![]() .
.
①当直线![]() ,
,![]() 的斜率都存在时,设过点
的斜率都存在时,设过点![]() 与椭圆
与椭圆![]() 相切的直线方程为
相切的直线方程为![]() .
.
由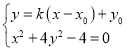 ,消去
,消去![]() ,
,
得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .∴
.∴![]() .
.
又![]() ,∴
,∴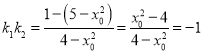 .
.
∴![]() ,即
,即![]() 为圆
为圆![]() 的直径,∴
的直径,∴![]() .
.
②当直线![]() 或
或![]() 的斜率不存在时,不妨设
的斜率不存在时,不妨设![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
∴![]() ,
,![]() ,也满足
,也满足![]() .
.
综上,有![]() .
.
(ii)设点![]() ,
,![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由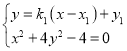 ,消去
,消去![]() ,得
,得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
则![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
化简可得![]() ,即
,即![]() .
.
经验证,当直线![]() 的斜率不存在时,
的斜率不存在时,
直线![]() 的方程为
的方程为![]() 或
或![]() ,也满足
,也满足![]() .
.
同理,可得直线![]() 的方程为
的方程为![]() .
.
∵![]() 在直线
在直线![]() ,
,![]() 上,∴
上,∴![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
由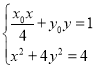 ,消去
,消去![]() ,得
,得![]() .
.
∴![]() ,
,![]() .
.
∴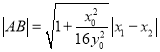
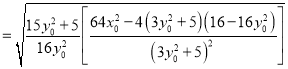
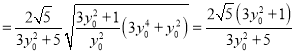 .
.
又点![]() 到直线
到直线![]() 的距离
的距离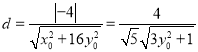 .
.
∴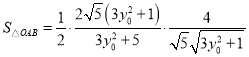
 .
.
令![]() ,
,![]() .则
.则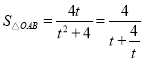 .
.
又![]() ,∴
,∴![]() 的面积的取值范围为
的面积的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为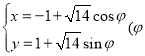 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 的交线为直线
的交线为直线![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点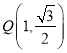 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)当直线![]() ,
,![]() 的斜率都存在时,记直线
的斜率都存在时,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(ii)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
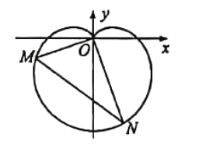
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线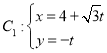 (t为参数),曲线
(t为参数),曲线![]() ,(
,(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 分别交
分别交![]() ,
,![]() 于A,B两点,求
于A,B两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
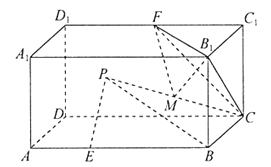
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com