
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,且
,且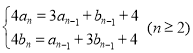
(1)令![]() 证明:
证明:![]() 是等差数列,
是等差数列,![]() 是等比数列;
是等比数列;
(2)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(3)求数列![]() 和
和![]() 的前n项和公式.
的前n项和公式.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】给定两个命题,p:对任意实数x都有x2+ax+1≥0恒成立;q:幂函数y=xa-1在(0,+∞)内单调递减;如果p与q中有且仅有一个为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() (公差不为零)和等差数列
(公差不为零)和等差数列![]() ,如果关于
,如果关于![]() 的实系数方程
的实系数方程![]() 有实数解,那么以下九个方程
有实数解,那么以下九个方程![]() (
(![]() )中,无实数解的方程最多有( )
)中,无实数解的方程最多有( )
A.3个B.4个C.5个D.6个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为: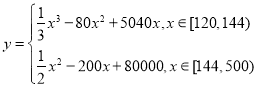 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为![]() 元,若该项目不获利,政府将给予补贴.
元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)设![]() ,若对一切正整数
,若对一切正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;.
的取值范围;.
(3)是否存在正整数![]() ,使得
,使得![]() 。成等比数列?若存在,求出所有的
。成等比数列?若存在,求出所有的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的递推公式
的递推公式
(2)数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明你的理由.
的取值范围;若不存在,请说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com